如图所示,一幢楼房AB背后有一台阶CD,台阶每层高 米,且AC=
米,且AC= 米,设太阳光线与水平地面的夹角为
米,设太阳光线与水平地面的夹角为 .当
.当 时,测得楼房在地面上的影长AE=
时,测得楼房在地面上的影长AE= 米,现有一只小猫睡在台阶的MN这层上晒太阳.(
米,现有一只小猫睡在台阶的MN这层上晒太阳.( 取
取 )
)
(1)求楼房的高度约为多少米?
(2)过了一会儿,当 时,问小猫能否还晒到太阳?请说明理由.
时,问小猫能否还晒到太阳?请说明理由.
如图,已知 是 的直径, 是 延长线上一点, 切 于点 , 是 的弦, ,垂足为 .
(1)求证: .
(2)过点 作 交 于点 ,交 于点 ,连接 ,若 , ,求 的长.

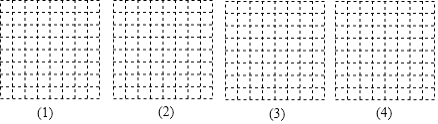
下面有4张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长都是1,请在方格纸中分别画出符合要求的图形,所画图形各顶点必须与方格纸中小正方形的顶点重合,具体要求如下:
(1)画一个直角边长为4,面积为6的直角三角形.
(2)画一个底边长为4,面积为8的等腰三角形.
(3)画一个面积为5的等腰直角三角形.
(4)画一个一边长为 ,面积为6的等腰三角形.
据调查, 超速行驶是引发交通事故的主要原因之一 . 小强用所学知识对一条笔直公路上的车辆进行测速, 如图所示, 观测点 到公路的距离 ,检测路段的起点 位于点 的南偏东 方向上, 终点 位于点 的南偏东 方向上 . 一辆轿车由东向西匀速行驶, 测得此车由 处行驶到 处的时间为 . 问此车是否超过了该路段 的限制速度? (观 测点 离地面的距离忽略不计, 参考数据: ,

某车行去年 型车的销售总额为6万元,今年每辆车的售价比去年减少400元.若卖出的数量相同,销售总额将比去年减少 .
(1)求今年 型车每辆车的售价.
(2)该车行计划新进一批 型车和 型车共45辆,已知 、 型车的进货价格分别是1100元、1400元,今年 型车的销售价格是2000元,要求 型车的进货数量不超过 型车数量的两倍,应如何进货才能使这批车获得最大利润,最大利润是多少?
某校为了解节能减排、垃圾分类等知识的普及情况,从该校2000名学生中随机抽取了部分学生进行调查,调查结果分为“非常了解“、“了解”、“了解较少”、“不了解”四类,并将调查结果绘制出以下两幅不完整的统计图.请根据统计图回答下列问题:

(1)本次调查的学生共有 人,估计该校2000名学生中“不了解”的人数约有 人.
(2)“非常了解”的4人中有 , 两名男生, , 两名女生,若从中随机抽取两人去参加环保知识竞赛,请用画树状图和列表的方法,求恰好抽到2名男生的概率.