如图，经过原点的抛物线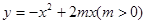
与
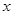轴的另一个交点为A.过点P(1,
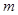)作直线PM⊥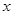轴于点M，交抛物线于点B．记点B关于抛物线对称轴的对称点为C(B、C不重合)．连结CB，CP．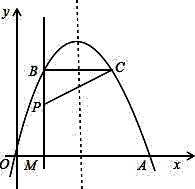
（1）当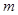＝3时，求点A的坐标和BC的长；
（2）当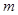>1时，连结CA，当CA⊥CP时，求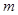的值．
（3）过点P作PE⊥PC且PE =PC，问是否存在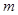，使得点E落x轴在上？若存在，求出所有满足要求的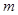的值，并写出相对应的点E坐标；若不存在，请说明理由．
解方程：
（1）
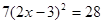
（2）
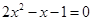
（3）
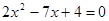（配方法）
（4）
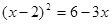
（本题10分）如果一个正整数能表示为两个连续偶数的平方差，那么称这个正整数为“和谐数”。如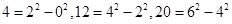
，因此4，12，20这三个数都是和谐数。
（1）36和2016这两个数是和谐数吗？为什么？
（2）设两个连续偶数为2k+2和2k（其中k取非负整数），由这两个连续偶数构造的和谐数是4的倍数吗？为什么？
（3）介于1到200之间的所有“和谐数”之和为 ．
（本题9分）把几个图形拼成一个新的图形，再通过图形面积的计算，常常可以得到一些有用的式子，或可以求出一些不规则图形的面积．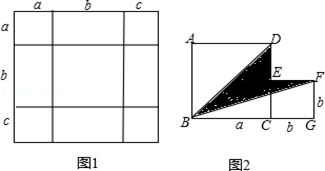
（1）如图1，是将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形，试用不同的形式表示这个大正方形的面积，你能发现什么结论，请用等式表示出来。
（2）如图2，是将两个边长分别为a和b的正方形拼在一起，B、C、G三点在同一直线上，连接BD和BF，若两正方形的边长满足a+b=10，ab=20，请求出阴影部分的面积。
（本题8分）阅读下列解题过程，然后解题：
题目：已知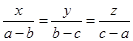
（a、b、c互不相等），求x+y+z的值．
解：设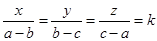
，则x=k（a-b），y=k（b-c），z=k（c-a），
∴x+y+z=k（a-b+b-c+c-a）=k•0=0，∴x+y+z=0．
依照上述方法解答下列问题：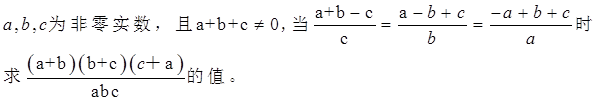
（本题6分）先化简（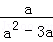
﹣
）÷
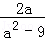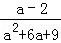，然后从不等式组
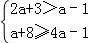的解集中选取一个你认为合适的整数作为a的值代入求值．