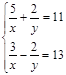已知:如图,抛物线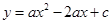 (
(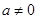 )与
)与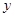 轴交于点
轴交于点 ( 0,4) ,与
( 0,4) ,与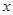 轴交于点
轴交于点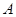 ,
,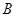 ,点
,点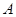 的坐标为(4,0).
的坐标为(4,0).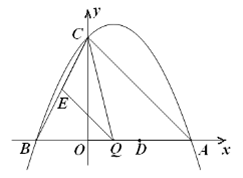
(1) 求该抛物线的解析式;
(2) 点 是线段
是线段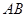 上的动点,过点
上的动点,过点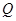 作
作 ∥
∥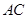 ,交
,交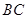 于点
于点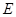 ,连接
,连接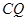 . 当
. 当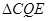 的面积最大时,求点
的面积最大时,求点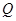 的坐标;
的坐标;
(3)若平行于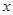 轴的动直线与该抛物线交于点
轴的动直线与该抛物线交于点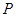 ,与直线
,与直线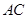 交于点
交于点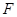 ,点
,点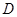 的坐标为(2,0). 问: 是否存在这样的直线,使得
的坐标为(2,0). 问: 是否存在这样的直线,使得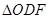 是等腰三角形?若存在,请求出点
是等腰三角形?若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
某运输部门规定:办理托运,当一件物品的重量不超过a千克(a<18)时,需付基础费30元和保险费b元;为了限制过重物品的托运,当一件物品超过a千克时,除了付以上基础费和保险费外,超过部分还需每千克付c元的超重费.设某件物品的重量为x千克当0<x≤a时,支付费用为___________(用含b的代数式表示);
当x>a时,支付费用为 ____________(用含x和a、b、c的代数式表示);甲、乙、丙三人各托运一件物品,物品的重量与支付费用如下表所示:

①根据以上提供的信息确定a、b、c的值;
②试问在物品可拆分的情况下,用不超过120元的费用能否托运50千克的物品?若能,请你设计出一种最省的托运方案;若不能,请你说明理由.
如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,则BE与DF有何位置关系?试说明理由.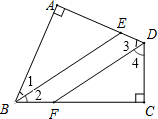
如图,AD为△ABC的中线,BE为△ABD的中线,
若∠ABE=25°,∠BAD=50°,则∠BED的度数是度
在△ADC中过点C画AD边上的高CH.
若△ABC的面积为20,BD=5,求点E到BC边的距离
先化简,再求值: ,其中
,其中 .
.
阅读理解:解方程组 时,如果设
时,如果设 ,则原方程组可变形为关于m、n的方程组
,则原方程组可变形为关于m、n的方程组 ,解这个方程组得到它的解为
,解这个方程组得到它的解为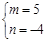 .由
.由 ,求得原方程组的解为
,求得原方程组的解为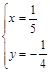 .利用上述方法解方程组:
.利用上述方法解方程组: