鄂州市化工材料经销公司购进一种化工原料若干千克,价格为每千 克30元.物价部门规定其销售单价不高于每千克60元,不低于每千克30元.经市场调查发现:日销售量y(千克)是销售单价x(元)的一次函数,且当x=60时 ,y=80;x=50时,y=100.在销售过程中,每天还要支付其他费用450元.
(1)求出y与x的函数关系式,并写出自变量x的取值范围.
(2)求该公司销售该原料日获利w(元)与销售单价x(元)之间的函数关系式.
(3)当销售单价为多少元时,该公司日获利最大?最大获利是多少元?
解不等式组: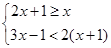 ,并将解集在数轴上表示出来.
,并将解集在数轴上表示出来.
如图,在△ABC中,AB=6,BC=9,AC=8,点P在△ABC内部,过点P分别画AB、BC、CA的平行线,与各边分别相交得线段DE、FG、HK,已知线段DE、FG、HK的长度都为d,求d的值.
已知关于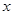 的方程
的方程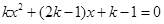 只有整数根,且关于
只有整数根,且关于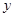 的一元二次方程
的一元二次方程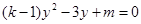 有两个实数根
有两个实数根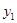 和
和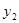 .
.
当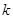 为整数时,确定
为整数时,确定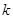 的值;
的值;
在(1)的条件下,若 且是整数,试求
且是整数,试求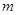 的最小值.
的最小值.
如图1,平面直角坐标系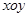 中,点
中,点 ,
,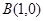 ,
,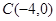 ,点
,点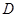 为射线
为射线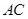 上一动点,连结
上一动点,连结 ,交
,交 轴于点
轴于点 ,⊙
,⊙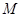 是△
是△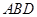 的外接圆,过点
的外接圆,过点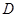 的切线交
的切线交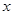 轴于点
轴于点 .
.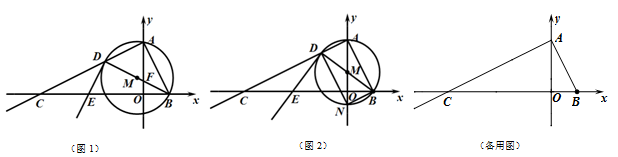
(1)判断△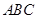 的形状;
的形状;
(2)当点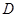 在线段
在线段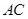 上时,
上时,
①证明:△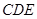 ∽△
∽△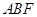 ;
;
②如图2,⊙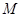 与
与 轴的另一交点为
轴的另一交点为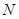 ,连结
,连结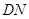 、
、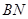 ,当四边形
,当四边形 为矩形时,求
为矩形时,求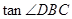 ;
;
(3)点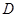 在射线
在射线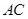 运动过程中,若
运动过程中,若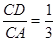 ,求
,求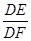 的值.
的值.
如图1,对于平面上不大于 的
的 ,我们给出如下定义:若点P在
,我们给出如下定义:若点P在 的内部或边界上,作
的内部或边界上,作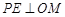 于点E,
于点E,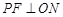 于点
于点 ,则称
,则称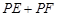 为点P相对于
为点P相对于 的“点角距离”,记为
的“点角距离”,记为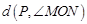 .
.
如图2,在平面直角坐标系xOy中,对于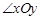 ,点P为第一象限内或两条坐标轴正半轴上的动点,且满足
,点P为第一象限内或两条坐标轴正半轴上的动点,且满足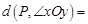 5,点P运动形成的图形记为图形G.
5,点P运动形成的图形记为图形G.
(1)满足条件的其中一个点P的坐标是__,图形G与坐标轴围成图形的面积等于__;
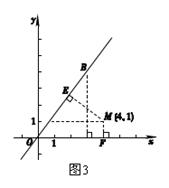
(2)设图形G与x轴的公共点为点A,如图3,已知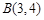 ,
,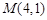 ,求
,求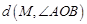 的值;
的值;
(3)如果抛物线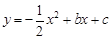 经过(2)中的A,B两点,点Q在A,B两点之间的物线上(点Q可与A,B两点重合),求当
经过(2)中的A,B两点,点Q在A,B两点之间的物线上(点Q可与A,B两点重合),求当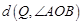 取最大值时,点Q 的坐标.
取最大值时,点Q 的坐标.