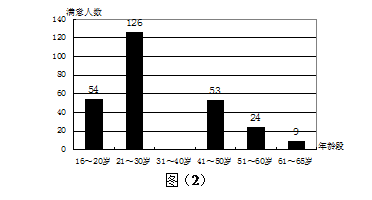
已知:如图①,在矩形ABCD中,AB=5,AD= ,AE⊥BD,垂足是E.点F是点E关于AB的对称点,连接AF、BF.
,AE⊥BD,垂足是E.点F是点E关于AB的对称点,连接AF、BF.
(1)求AE和BE的长;
(2)若将△ABF沿着射线BD方向平移,设平移的距离为m(平移距离指点B沿BD方向所经过的线段长度).当点F分别平移到线段AB、AD上时,直接写出相应的m的值.
(3)如图②,将△ABF绕点B顺时针旋转一个角 (0°<
(0°< <180°),记旋转中的△ABF为△A′BF′,在旋转过程中,设A′F′所在的直线与直线AD交于点P.与直线BD交于点Q.是否存在这样的P、Q两点,使△DPQ为等腰三角形?若存在,求出此时DQ的长;若不存在,请说明理由.
<180°),记旋转中的△ABF为△A′BF′,在旋转过程中,设A′F′所在的直线与直线AD交于点P.与直线BD交于点Q.是否存在这样的P、Q两点,使△DPQ为等腰三角形?若存在,求出此时DQ的长;若不存在,请说明理由.
将□ABCD纸片沿EF折叠,使点C与点A重合,点D落在点G处.求证:△ABE≌△AGF.
连结AC,若□ABCD的面积等于8,
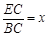 ,
,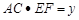 ,试求y与x之间的函数关系式.
,试求y与x之间的函数关系式.
如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C.用直尺和圆规画出该圆弧所在圆的圆心M的位置(不用写作法,保留作图痕迹).
若A点的坐标为(0,4),D点的坐标为(7,0),直线CD与⊙M的位置关系为________,再连结MA、MC,将扇形AMC卷成一个圆锥,求此圆锥的侧面积.
为了帮助日本地震灾区重建家园,某公司号召员工自愿捐款.请你根据两位经理的对话,计算出第一次捐款的人数.
如图,有一块含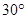 的直角三角板
的直角三角板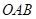 的直角边长
的直角边长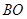 的长恰与另一块等腰直角三角板
的长恰与另一块等腰直角三角板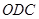 的斜边
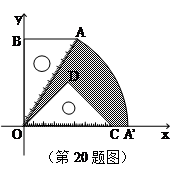
的斜边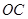 的长相等,把该套三角板放置在平面直角坐标系中,且
的长相等,把该套三角板放置在平面直角坐标系中,且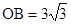 .
.若双曲线的一个分支恰好经过点
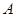 ,求双曲线的解析式;
,求双曲线的解析式;若把含
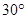 的直角三角板绕点
的直角三角板绕点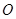 按顺时针方向旋转后,斜边
按顺时针方向旋转后,斜边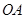 恰好与
恰好与 轴重叠,点
轴重叠,点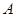 落在点
落在点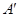 ,试求图中阴影部分的面积(结果保留
,试求图中阴影部分的面积(结果保留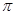 ).
).
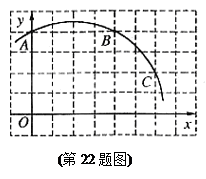
某市为了解市民对已闭幕的某一博览会的总体印象,利用最新引进的“计算机辅助电话访问系统”(简称CATI系统),采取电脑随机抽样的方式,对本市年龄在16~65岁之间的居民,进行了400个电话抽样调查.并根据每个年龄段的抽查人数和该年龄段对博览会总体印象感到满意的人数绘制了下面的图(1)和图(2)(部分)
根据上图提供的信息回答下列问题:被抽查的居民中,人数最多的年龄段是 岁;
已知被抽查的400人中有83%的人对博览会总体印象感到满意,请你求出31~40岁年龄段的满意人数,并补全图(2);
比较31~40岁和41~50岁这两个年龄段对博览会总体印象满意率的高低(四舍五入到1%).注:某年龄段的满意率=该年龄段满意人数
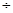 该年龄段被抽查人数
该年龄段被抽查人数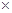 100%.
100%.