已知向量 ,
,
设函数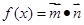 +
+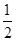 (1)若
(1)若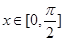 ,f(x)=
,f(x)=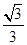 ,求
,求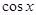 的值; (2)在△ABC中,角A,B,C的对边分别是
的值; (2)在△ABC中,角A,B,C的对边分别是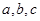 ,且满足
,且满足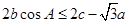 ,求f(B)的取值范围.
,求f(B)的取值范围.
选修4—4:坐标系与参数方程
已知曲线C1的极坐标方程为 ,曲线C2的极坐标方程为
,曲线C2的极坐标方程为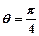 (
(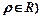 ,曲线C1,C2相交于点A,B。
,曲线C1,C2相交于点A,B。
(1)将曲线C1,C2的极坐标方程化为直角坐标方程;
(2)求弦AB的长。
选修4-1:几何证明选讲
如图,圆O的直径AB=10,弦DE⊥AB于点H,AH=2。
(1)求DE的长;
(2)延长ED到P,过P作圆O的切线,
切点为C,若PC=2 ,求PD的长。
,求PD的长。
(本小题满分14分)
等差数列 的各项均为正数,
的各项均为正数,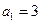 ,前
,前 项和为
项和为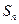
 ,
,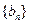 为等比数列,
为等比数列, 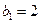 ,且
,且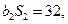
 .
.
(1)求 与
与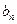 ;
;
(2)求数列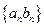 的前
的前 项和
项和 。
。
(3)若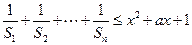 对任意正整数
对任意正整数 和任意
和任意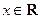 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分14分)
已知函数
(1)若 ,求
,求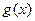
 的单调递减区间;
的单调递减区间;
(2)若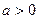 ,且存在
,且存在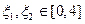 使得
使得 ,求实数
,求实数 的取值范围。
的取值范围。
已知角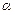 的顶点在原点,始边与
的顶点在原点,始边与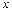 轴的正半轴重合,终边经过点
轴的正半轴重合,终边经过点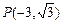 .
.
(1)求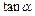 的值;
的值;
(2)定义行列式运算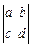
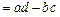 ,求行列式
,求行列式 的值;
的值;
(3)若函数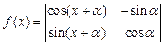 (
( ),求函数
),求函数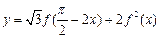 的最大值,并指出取到最大值时
的最大值,并指出取到最大值时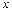 的值.
的值.