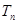如图所示, 四棱锥P-ABCD的底面是边长为1的正方形,PA^CD,PA = 1,PD= ,E为PD上一点,PE = 2ED.
,E为PD上一点,PE = 2ED.
(1)求证:PA ^平面ABCD;
(2)求二面角D-AC-E的余弦值;
(3)在侧棱PC上是否存在一点F,使得BF // 平面AEC?
若存在,指出F点的位置,并证明;若不存在,说明理由.
某校高一年级开设 ,
, ,
, ,
, ,
, 五门选修课,每位同学须彼此独立地选三门课程,其中甲同学必选
五门选修课,每位同学须彼此独立地选三门课程,其中甲同学必选 课程,不选
课程,不选 课程,另从其余课程中随机任选两门课程.乙、丙两名同学从五门课程中随机任选三门课程.
课程,另从其余课程中随机任选两门课程.乙、丙两名同学从五门课程中随机任选三门课程.
(Ⅰ)求甲同学选中 课程且乙同学未选中
课程且乙同学未选中 课程的概率;
课程的概率;
(Ⅱ)用 表示甲、乙、丙选中
表示甲、乙、丙选中 课程的人数之和,求
课程的人数之和,求 的分布列和数学期望.
的分布列和数学期望.
已知函数 .
.
(Ⅰ)求 的定义域及其最大值;
的定义域及其最大值;
(Ⅱ)求 在
在 上的单调递增区间.
上的单调递增区间.
已知等差数列 的首项
的首项 ,公差
,公差 >0,前
>0,前 项和
项和
(1)若 ,
, ,
, 成等比数列,求数列
成等比数列,求数列 的前
的前 项和
项和 ;
;
(2)若 >
> 对一切
对一切 恒成立,求
恒成立,求 的取值范围。
的取值范围。
在△ABC中, 、
、 、
、 分别是三个内角A、B、C的对边,若向量
分别是三个内角A、B、C的对边,若向量 =
= 与向量
与向量 共线
共线
(1)求角A;
(2)若 =2,求
=2,求 得取值范围。
得取值范围。
已知数列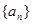 的前
的前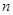 项和
项和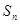 ,且
,且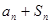 =1
=1
(1)证明数列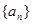 是等比数列;
是等比数列;
(2)若数列{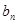 }满足
}满足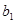 =1,
=1,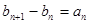 ,求数列{
,求数列{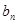 }的前
}的前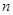 项和
项和