如图所示,半径为R的3/4圆周轨道固定在竖直平面内,O为圆轨道的圆心,D为圆轨道的最高点,圆轨道内壁光滑,圆轨道右侧的水平面BC与圆心等高。质量为m的小球从离B点高度为h处的A点由静止开始下落,从B点进入圆轨道,小球能通过圆轨道的最高点,并且在最高点对轨道的额压力不超过3mg。现由物理知识推知,小球下落高度h与圆轨道半径R及小球经过D点时的速度vD之间的关系为 。
。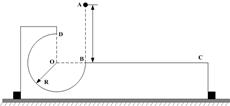
(1)求高度h应满足的条件;
(2)通过计算说明小球从D点飞出后能否落在水平面BC上,并求落点与B点水平距离的范围。
一辆汽车在平路上以速度为36 km/h行驶,它以这个速度开始下坡,5s后到达坡底时速度为72km/h.,设下坡过程汽车做匀变速直线运动,求它下坡的加速度与坡长
一物体从某时刻起做匀加速直线运动,已知其初速度v0=4m/s,加速度a=2m/s2,求:2s末物体速度的大小;
开始运动后2s内物体位移的大小。
某运动员在百米跑道上以8m/s的速度跑了80m,然后又以2m/s的速度走了20m,这个运动员通过这段路的平均速度是多少?
光滑水平面上有一质量为M、长度为L的木板AB,在木板的中点有一质量为m的小木块,木板上表面是粗糙的,它与木块间的动摩擦因数为μ.开始时两者均处于静止状态,现在木板的B端加一个水平向右的恒力F,则:
木板和木块运动的加速度是多大?
若在木板的B端到达距右方距离为L的P点前,木块能从本板上滑出,则水平向右的恒力F应满足什么条件?
如图所示是建筑工地常用的一种“深穴打夯机”,电动机带动两个滚轮匀速转动将静止的夯杆从深坑提上来,当夯杆底端刚到达坑口时,两个滚轮彼此分开,将夯杆释放,夯杆在重力作用下落回深坑,夯实坑底。如此循环往复。已知两个滚轮边缘的线速度恒为v=4m/s,每个滚轮对夯杆的压力FN=2×104N,滚轮与夯杆间的动摩擦因数μ=O.3,夯杆质量m=1×103kg,坑深h="6.4" m,取g=IOm/s2。求: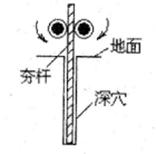
夯杆自坑底开始匀加速上升,当速度增加到4m/s时,夯杆上升的高度;
夯杆自坑底上升的最大高度;
夯杆往复运动的周期。