在矩形ABCD中,DC=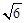 ,CF⊥BD分别交BD、AD于点E、F,连接BF.
,CF⊥BD分别交BD、AD于点E、F,连接BF.
(1)求证:△DEC∽△FDC;
(2)当F为AD的中点时,求sin∠FBD的值及BC的长度.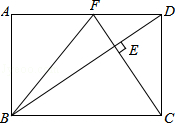
(本小题满分10分)已知代数式:A=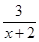 ,B=
,B=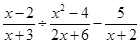 .
.
(1)试证明:若A、B均有意义,则它们的值互为相反数;
(2)若代数式A、B中的x是满足不等式3(x-3)<6-2x的正整数解,求A-B的值.
如图,已知抛物线 与x轴交于A(-2,0)、B两点,与y轴交于C点,其对称轴为直线
与x轴交于A(-2,0)、B两点,与y轴交于C点,其对称轴为直线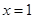 .
.
(1)求抛物线的解析式;
(2)把线段AC沿x轴向右平移,设平移后A、C的对应点分别为A′、C′,当C′落在抛物线上时,求A′、C′的坐标;
(3)除(2)中的点A′、C′外,在x轴和抛物线上是否还分别存在点E、F,使得以A、C、E、F为顶点的四边形为平行四边形,若存在,求出E、F的坐标;若不存在,请说明理由.
如图1所示,将一个边长为2的正方形ABCD和一个长为2、宽为1的矩形CEFD拼在一起,构成一个大的长方形ABEF.现将小长方形CEFD绕点C顺时针旋转至CE′F′D,旋转角为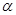 .
.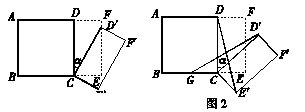
(1)当点D′恰好落在EF边上时,则旋转角α的值为________度;
(2)如图2,G为BC中点,且0°<α<90°,求证:GD′=E′D;
(3)小长方形CEFD绕点C顺时针旋转一周的过程中,是否存在旋转角α,使△DCD′与△CBD′全等?若能,直接写出旋转角α的值;若不能,说明理由.
如图,点C在⊙O的直径AB的延长线上,点D在⊙O上,AD=CD,∠ADC=120°.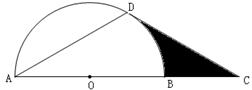
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.
某市“艺术节”期间,小明、小亮都想去观看茶艺表演,但是只有一张茶艺表演门票,他们决定采用抽卡片的办法确定谁去,规定如下:将正面分别标有数字1、2、3、4的四张卡片(除数字外其余都相同)洗匀后,背面朝上放置在桌面上,随机抽出一张记下数字后放回,重新洗匀后背面朝上放置在桌面上,再随机抽出一张记下数字,如果两个数字的和为奇数,则小明去;如果两个数字的和为偶数,则小亮去.
(1)请用列表或画树形图(树状图)的方法表示抽出的两张卡片上的数字和的所用可能出现的结果;
(2)你认为这个规则公平吗?请说明理由.