如图1是一张折叠椅子，图2是其侧面示意图，已知椅子折叠时长1.2米，椅子展开后最大张角∠CBD＝37°，且BD＝BC，AB：BG：GC＝1：2：3，座面EF与地面平行，当展开角最大时，请解答下列问题：
（1）求∠CGF的度数；
（2）求座面EF与地面之间的距离。（可用计算器计算，结果保留两个有效数字，参考数据：sin71.5°≈0.948，cos71.5°≈0.317，tan71.5°≈2.989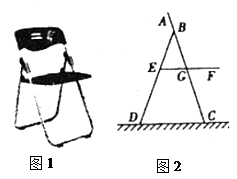
如图，在□ABCD中，E、F为对角线BD上的两点，且BE=DF．求证：∠BAE=∠DCF．
在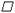
ABCD中，对角线AC与BD交于点O，∠BAD的平分线交直线BC于点E，交直线DC于点F.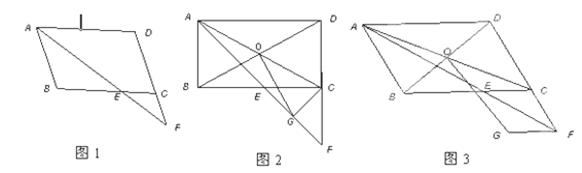
（1）在图1中，证明CE=CF；
（2）若，∠BAD=90°， G是EF的中点（如图2），连结OG，判断OG与BD的位置关系与数量关系，并给出证明；
（3）若∠ABC=120°，FG∥CE，FG=CE，连结OG（如图3），判断OG与BD的位置关系与数量关系，并给出证明.
如图，梯形ABCD中，AD//BC，BC＝5，AD＝3，对角线AC⊥BD，且∠DBC＝30°，求梯形ABCD的高。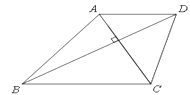 
正方形ABCD中，点E、F为对角线BD上两点，DE=BF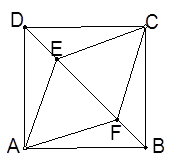
（1）四边形AECF是什么四边形？ 为什么？
（2）若EF=4cm，DE=BF=2cm，求四边形AECF的周长。
如图，一次函数
的图像与反比例函数
的图像相交于A、B两点，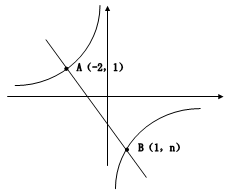
（1）利用图中条件，求反比例函数和一次函数的解析式；
（2）根据图像回答：当x取何值时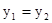
（3）根据图像回答：当x取何值时