已知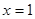 是函数
是函数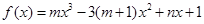 的一个极值点,其中
的一个极值点,其中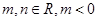 .
.
(1)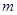 与
与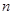 的关系式;
的关系式;
(2)求 的单调区间;
的单调区间;
(3)当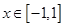 时,函数
时,函数 的图象上任意一点处的切线的斜率恒大于
的图象上任意一点处的切线的斜率恒大于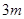 ,求
,求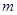 的取值范围.
的取值范围.
如图,在直三棱柱ABC﹣A1B1C1中,AB=2,AC=AA1=4,∠ABC=90°.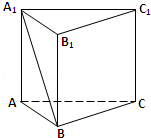
(1)求三棱柱ABC﹣A1B1C1的表面积S;
(2)求异面直线A1B与AC所成角的余弦值.
甲、乙两家商场对同一种商品开展促销活动,对购买该商品的顾客两家商场的奖励方案如下:
甲商场:顾客转动如图所示圆盘,当指针指向阴影部分(图中四个阴影部分均为扇形,且每个扇形圆心角均为15°,边界忽略不计)即为中奖.
乙商场:从装有3个白球3个红球的盒子中一次性摸出2球(球除颜色外不加区分),如果摸到的是2个红球,即为中奖.
问:购买该商品的顾客在哪家商场中奖的可能性大?
已知函数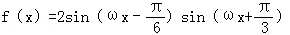 (其中ω为正常数,x∈R)的最小正周期为π.
(其中ω为正常数,x∈R)的最小正周期为π.
(1)求ω的值;
(2)在△ABC中,若A<B,且 ,求
,求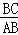 .
.
(本小题满分14分)已知函数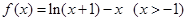 .
.
(1)求 的单调区间;
的单调区间;
(2)已知数列 的通项公式为
的通项公式为 ,求证:
,求证: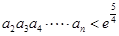 (
( 为自然对数的底数);
为自然对数的底数);
(3)若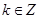 ,且
,且 对任意
对任意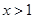 恒成立,求
恒成立,求 的最大值
的最大值
(本小题满分13分)已知等差数列 的前
的前 项和为
项和为 ,并且
,并且 ,
,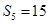 ,数列
,数列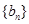 满足:
满足: ,
, ,记数列
,记数列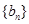 的前
的前 项和为
项和为 .
.
(1)求数列 的通项公式
的通项公式 及前
及前 项和公式
项和公式 ;
;
(2)求数列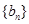 的通项公式
的通项公式 及前
及前 项和公式
项和公式 ;
;
(3)记集合 ,若
,若 的子集个数为16,求实数
的子集个数为16,求实数 的取值范围
的取值范围