已知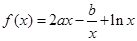 在
在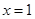 与
与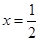 处都取得极值.
处都取得极值.
(1)求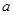 ,
,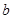 的值;
的值;
(2)设函数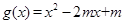 ,若对任意的
,若对任意的 ,总存在
,总存在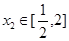 ,使得、
,使得、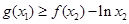 ,求实数
,求实数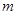 的取值范围.
的取值范围.
设函数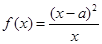 .
.
(I)证明: 是函数
是函数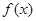 在区间
在区间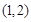 上递增的充分而不必要的条件;
上递增的充分而不必要的条件;
(II)若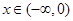 时,满足
时,满足 恒成立,求实数
恒成立,求实数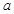 的取值范围.
的取值范围.
某商场预计2013年1月份起前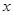 个月,顾客对某种商品的需求总量
个月,顾客对某种商品的需求总量 (单位:件)与
(单位:件)与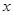 的关系近似地满足:
的关系近似地满足: .该商品第
.该商品第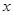 月的进货单价
月的进货单价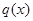 (单位:元)与x的近似关系是:
(单位:元)与x的近似关系是: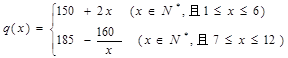
(1)写出今年第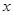 月的需求量
月的需求量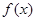 件与
件与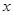 的函数关系式;
的函数关系式;
(2)该商品每件的售价为185元,若不计其他费用且每月都能满足市场需求,试问商场2013年第几月份销售该商品的月利润最大,最大月利润为多少元?
数列 中,
中,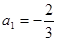 ,其前n项和
,其前n项和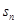 满足
满足
 ,
,
(1)计算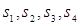 ;
;
(2)猜想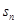 的表达式并用数学归纳法证明。
的表达式并用数学归纳法证明。
设 .
.
(1)求 的单调区间;
的单调区间;
(2)求函数 在
在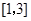 上的最值.
上的最值.
已知函数 .
.
(1)求函数 的单调区间;
的单调区间;
(2)若直线 与函数
与函数 的图像有
的图像有 个交点,求
个交点,求 的取值范围.
的取值范围.