某研究性学习小组有
名同学．
（1）这名同学排成一排照相，则同学甲与同学乙相邻的排法有多少种？
（2）从名同学中选
人参加班级
接力比赛，则同学丙不跑第一棒的安排方法有多少种？
设x1,x2是关于x的一元二次方程x2－2(m－1)x＋m＋1=0的两个实根，又y=x21＋x22，求y=f(m)的解析式及此函数的定义域.
设函数
，
（1）求
的定义域；
（2）是否存在最大值或最小值？如果存在，请把它求出来；若不存在，请说明理由.
某工厂今年1月、2月、3月生产某产品分别为1万件，1.2万件， 1.3万件，为了估计以后每月的产量，以这三个月的产量为依据，用一个函数模拟该产品的月产量y与月份x的关系，模拟函数可以选用二次函数或函数y=a·bx＋c(a,b,c)为常数。已知四月份该产品的产量为1.37万件，请问用以上哪个函数作模拟函数较好？说明理由.
设函数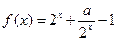
（a为实数）
（1）当a＝0时，若函数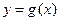
的图象与
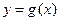的图象关于直线x=1对称，求函数的解析式；
（2）当a<0时，求关于x的方程＝0在实数集R上的解.
设函数f(x)对任意x,y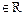
，都有
，且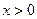
时，f(x)<0，f(1)=－2．
⑴求证：f(x)是奇函数；
⑵试问在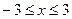
时，f(x)是否有最值？如果有求出最值；如果没有，说出理由.