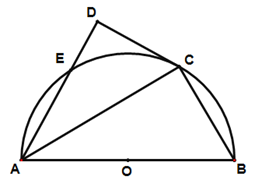
已知 为半圆
为半圆 的直径,
的直径,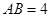 ,
,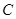 为半圆上一点,过点
为半圆上一点,过点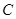 作半圆的切线
作半圆的切线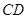 ,过
,过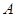 点作
点作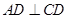 于
于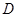 ,交半圆于点
,交半圆于点 ,
,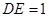 .
.
(1)证明: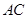 平分
平分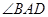 ;
;
(2)求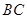 的长.
的长.
已知函数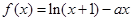 在
在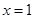 处的切线的斜率为
处的切线的斜率为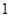 .
.
(1)求实数 的值及函数
的值及函数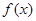 的最大值;
的最大值;
(2)证明: .
.
已知椭圆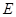 的中心在原点,焦点在
的中心在原点,焦点在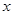 轴上,椭圆上的点到焦点的最小距离为
轴上,椭圆上的点到焦点的最小距离为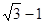 ,离心率
,离心率 .
.
(1)求椭圆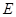 的方程;
的方程;
(2)若直线 交
交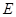 于
于 、
、 两点,点
两点,点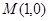 ,问是否存在
,问是否存在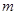 ,使
,使 ?若存在求出
?若存在求出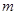 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
等边三角形 的边长为3,点
的边长为3,点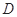 、
、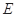 分别是边
分别是边 、
、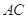 上的点,且满足
上的点,且满足
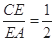 (如图1).将△
(如图1).将△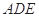 沿
沿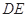 折起到△
折起到△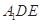 的位置,使二面角
的位置,使二面角 成直二面角,连结
成直二面角,连结 、
、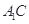 (如图2).
(如图2).
(1)求证: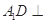 平面
平面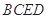 ;
;
(2)在线段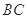 上是否存在点
上是否存在点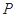 ,使直线
,使直线 与平面
与平面 所成的角为
所成的角为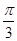 ?若存在,求出
?若存在,求出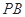 的长,若不存在,请说明理由.
的长,若不存在,请说明理由.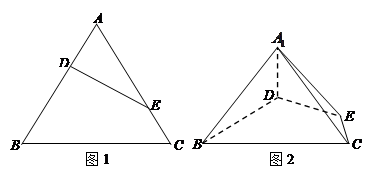
(本题满分12分 )
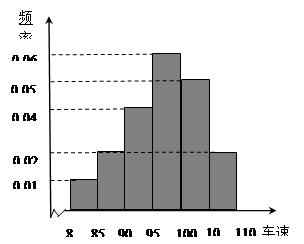
2013年国庆期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段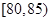 ,
,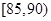 ,
,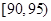 ,
,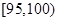 ,
, ,
,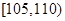 后得到如下图的频率分布直方图.
后得到如下图的频率分布直方图.
(1)此调查公司在采样中,用到的是什么抽样方法?
(2)求这40辆小型车辆车速的中位数的估计值;
(3)若从车速在 的车辆中任抽取3辆,求抽出的3辆车中车速在
的车辆中任抽取3辆,求抽出的3辆车中车速在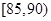 的车辆数
的车辆数 的分布列及数学期望.
的分布列及数学期望.