如图1,在平面直角坐标系中,等腰Rt△AOB的斜边OB在x轴上,直线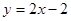 经过等腰Rt△AOB的直角顶点A,交y轴于C点.
经过等腰Rt△AOB的直角顶点A,交y轴于C点.
(1) 求点A坐标;
(2)若点P为x轴上一动点.点Q的坐标是(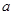 ,
,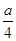 ),△PAQ是以点A为直角顶点的等腰三角形.求出
),△PAQ是以点A为直角顶点的等腰三角形.求出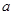 的值并写出点Q的坐标.
的值并写出点Q的坐标.
(3)在(2)的条件下,若D是坐标平面内任意一点,使点A、P、Q、D刚好能构成平行四边形,请直接写出符合条件的点D的坐标
.

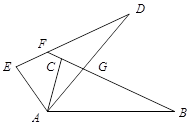
如图,在Rt△ABC中,∠ACB=90°,E为AC上一点,且AE=BC,过点A作AD⊥CA,垂足为A,且AD=AC,AB、DE交于点F.
(1)判断线段AB与DE的数量关系和位置关系,并说明理由;
(2)连接BD、BE,若设BC=a,AC=b,AB=c,请利用四边形ADBE的面积证明勾股定理.
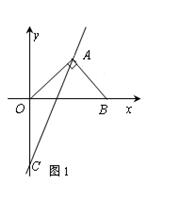
如图,在△ABC中,AC边的垂直平分线DM交AC于D,BC边的垂直平分线EN交BC于E,DM与EN相交于点F.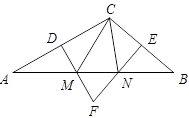
(1)若△CMN的周长为20cm,求AB的长;
(2)若∠MFN=70°,求∠MCN的度数.
如图,在四边形ABCD中,∠BAD=∠BCD=90°,M、N分别是BD、AC的中点.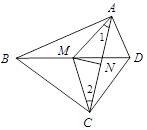
(1)求证:MN⊥AC;
(2)若∠ADC=120°,求∠1的度数.
如图,在△ABC中,AB=AC,点D是BC的中点,AB平分∠DAE,AE⊥BE,垂足为E.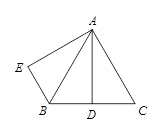
(1)求证:AD=AE;
(2)若BE∥AC,试判断△ABC的形状,并说明理由.
如图,△ABC≌△ADE,∠EAB =125°,∠CAD=25°,求∠BFD的度数.