在平面直角坐标系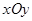 中,已知抛物线
中,已知抛物线 :
: ,在此抛物线上一点
,在此抛物线上一点
 到焦点的距离是3.
到焦点的距离是3.
(1)求此抛物线的方程;
(2)抛物线 的准线与
的准线与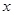 轴交于
轴交于 点,过
点,过 点斜率为
点斜率为 的直线
的直线 与抛物线
与抛物线 交于
交于 、
、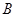 两点.是否存在这样的
两点.是否存在这样的 ,使得抛物线
,使得抛物线 上总存在点
上总存在点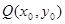 满足
满足 ,若存在,求
,若存在,求 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
(本小题满分16分)在直角坐标平面中,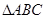 的两个顶点为
的两个顶点为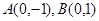 ,平面内两点
,平面内两点 同时满足:
同时满足:
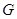 为
为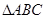 的重心;
的重心;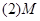 到
到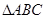 三点
三点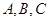 的距离相等;
的距离相等;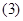 直线
直线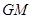 的倾斜角为
的倾斜角为 .
.
(1)求证:顶点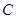 在定椭圆
在定椭圆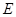 上,并求椭圆
上,并求椭圆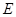 的方程;
的方程;
(2)设 都在曲线
都在曲线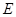 上,点
上,点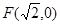 ,直线
,直线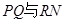 都过点
都过点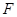 并且相互垂直,求四边形
并且相互垂直,求四边形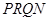 的面积
的面积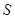 的最大值和最小值.
的最大值和最小值.
(本小题满分16分)
(1)求右焦点坐标是 ,且经过点
,且经过点 的椭圆的标准方程.
的椭圆的标准方程.
(2)已知椭圆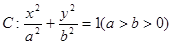 ,设斜率为
,设斜率为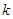 的直线
的直线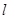 交椭圆
交椭圆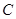 于
于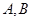 两点,
两点, 的中点为
的中点为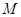 ,证明:当直线
,证明:当直线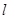 平行移动时,动点
平行移动时,动点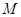 在一条过原点的定直线上.
在一条过原点的定直线上.
(3)利用(2)中所揭示的椭圆几何性质,用作图方法找出图中的定椭圆的中心,简要写出作图步骤,并在图中标出椭圆的中心.
(本小题满分15分)学校科技小组在计算机上模拟航天器变轨返回试验.设计方案如图:航天器运行(按顺时针方向)的轨迹方程为 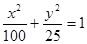 ,变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以y轴为对称轴、
,变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以y轴为对称轴、 为顶点的抛物线的实线部分,降落点为
为顶点的抛物线的实线部分,降落点为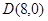 .观测点
.观测点 ,
, 同时跟踪航天器.
同时跟踪航天器.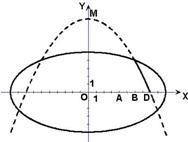
(1)求航天器变轨后的运行轨迹所在的曲线方程;
(2)试问:当航天器在x轴上方时,观测点A、B测得离航天器的距离分别为多少时,应向航天器发出变轨指令?
(本小题满分15分)如图,在四棱柱 中,已知平面
中,已知平面 ,
,
且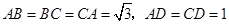 .
.
(1)求证: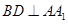 ;
;
(2)在棱BC上取一点E,使得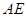 ∥平面
∥平面 ,求
,求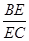 的值.
的值.
如图,在四棱锥P‐ABCD中,四边形ABCD为正方形,PA⊥平面ABCD,E为PD的中点.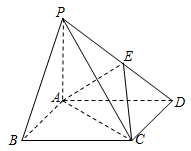
求证:(1)PB∥平面AEC;(2)平面PCD⊥平面PAD.