(本小题满分12分)递增等比数列{an}中a1=2,前n项和为Sn,S2是a2,a3的等差中项:(Ⅰ)求Sn及an;(Ⅱ)数列{bn}满足 的前n项和为Tn,求
的前n项和为Tn,求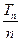 的最小值.
的最小值.
(本小题满分13分)在三角形ABC中,∠A,∠B,∠C的对边分别为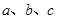 且
且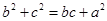
(1)求∠A;
(2)若 ,求
,求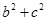 的取值范围.
的取值范围.
已知数列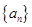 的前
的前 项和为
项和为 ,点
,点 均在二次函数
均在二次函数 的图象上.
的图象上.
(1)求数列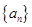 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前
的前 项和
项和
(本题10分)已知直线
(1)若直线 的斜率等于2,求实数
的斜率等于2,求实数 的值;
的值;
(2)若直线 分别与x轴、y轴的正半轴交于A、B两点,O是坐标原点,求△AOB面积的最大值及此时直线的方程.
分别与x轴、y轴的正半轴交于A、B两点,O是坐标原点,求△AOB面积的最大值及此时直线的方程.
(本题13分)已知ABCD是矩形,AD=4,AB=2,E、F分别是线段AB、BC的中点,PA⊥平面ABCD.
(1)求证:PF⊥FD;
(2)设点G在PA上,且EG//平面PFD,试确定点G的位置.
(本小题满分13分)数列{ }的前
}的前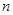 项和为
项和为 ,
, 是
是 和
和 的等差中项,等差数列{
的等差中项,等差数列{ }满足
}满足 ,
, .
.
(1)求数列 ,
, 的通项公式;
的通项公式;
(2)若 ,求数列
,求数列 的前
的前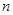 项和
项和