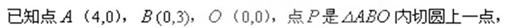

(本小题满分12分)
对于函数f(x),若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点。如果函数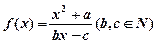 有且只有两个不动点0,2,且
有且只有两个不动点0,2,且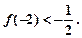
(1)求函数f(x)的解析式;
(2)已知各项不为零的数列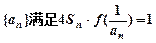 (
(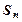 为
为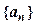 数列前n项和),求数列通项
数列前n项和),求数列通项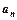 ;
;
(3)如果数列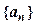 满足
满足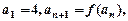 ,求证:当
,求证:当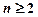 时,恒有
时,恒有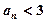 成立.
成立.
已知椭圆
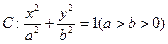 过点
过点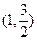 ,且离心率
,且离心率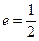 ,
,
(Ⅰ)求椭圆方程;
(Ⅱ)若直线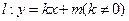 与椭圆交于不同的两点
与椭圆交于不同的两点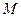 .
.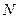 ,且线段
,且线段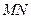 的垂直平分线过定点
的垂直平分线过定点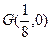 ,求
,求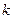 的取值范围。
的取值范围。
数列{an}满足a1=1,a2=2,an+2=(1+cos2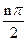 )an+sin
)an+sin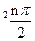 ,n=1.2.3…
,n=1.2.3…
(1)求a3.a4并求数列{an}的通项公式
(2)设bn=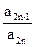 ,令 Sn=
,令 Sn=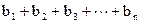 ,求 Sn
,求 Sn
(本小题满分13分)设圆C满足:(1)截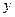 轴所得弦长为2;(2)被
轴所得弦长为2;(2)被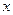 轴分成两段圆弧,其弧长的比为5∶1.在满足条件(1).(2)的所有圆中,求圆心到直线
轴分成两段圆弧,其弧长的比为5∶1.在满足条件(1).(2)的所有圆中,求圆心到直线
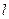 :3
:3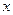 -4
-4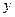 =0的距离最小的圆的方程.
=0的距离最小的圆的方程.
(本小题满分13分)已知函数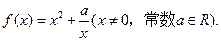
(Ⅰ)当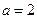 时,解不等式
时,解不等式 >
> ;
;
(Ⅱ)讨论函数 的奇偶性,并说明理由.
的奇偶性,并说明理由.