已知f(x)=x+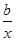 -3,x∈[1,2].
-3,x∈[1,2].
(1)当b=2时,求f(x)的值域;
(2)若b为正实数,f(x)的最大值为M,最小值为m,且满足M-m≥4,求b的取值范围.
【2015高考上海,文20】本题共2小题,第1小题6分,第2小题8分.
已知函数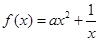 ,其中
,其中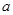 为实数.
为实数.
(1)根据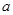 的不同取值,判断函数
的不同取值,判断函数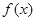 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)若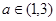 ,判断函数
,判断函数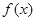 在
在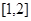 上的单调性,并说明理由.
上的单调性,并说明理由.
【2015高考上海,理20】如图,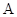 ,
,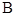 ,
,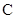 三地有直道相通,
三地有直道相通, 千米,
千米, 千米,
千米, 千米.现甲、乙两警员同时从
千米.现甲、乙两警员同时从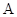 地出发匀速前往
地出发匀速前往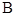 地,经过
地,经过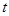 小时,他们之间的距离为
小时,他们之间的距离为 (单位:千米).甲的路线是
(单位:千米).甲的路线是 ,速度为
,速度为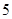 千米/小时,乙的路线是
千米/小时,乙的路线是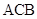 ,速度为
,速度为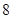 千米/小时.乙到达
千米/小时.乙到达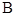 地后原地等待.设
地后原地等待.设 时乙到达
时乙到达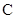 地.
地.
(1)求 与
与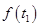 的值;
的值;
(2)已知警员的对讲机的有效通话距离是 千米.当
千米.当 时,求
时,求 的表达式,并判断
的表达式,并判断 在
在 上得最大值是否超过
上得最大值是否超过 ?说明理由.
?说明理由.
【2015高考浙江,理18】已知函数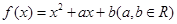 ,记
,记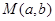 是
是 在区间
在区间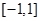 上的最大值.
上的最大值.
(1)证明:当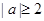 时,
时,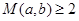 ;
;
(2)当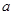 ,
,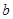 满足
满足 ,求
,求 的最大值.
的最大值.
如图,已知椭圆 与
与 的中心在坐标原点
的中心在坐标原点 ,长轴均为
,长轴均为 且在
且在 轴上,短轴长分别为
轴上,短轴长分别为 ,
,
 ,过原点且不与
,过原点且不与 轴重合的直线
轴重合的直线 与
与 ,
, 的四个交点按纵坐标从大到小依次为
的四个交点按纵坐标从大到小依次为 、
、 、
、 、
、 .记
.记 ,
, 和
和 的面积分别为
的面积分别为 和
和 .
.
(1)当直线 与
与 轴重合时,若
轴重合时,若 ,求
,求 的值;;
的值;;
(2)设直线 ,若
,若 ,证明:
,证明: 是线段
是线段 的四等分点
的四等分点
(3)当 变化时,是否存在与坐标轴不重合的直线
变化时,是否存在与坐标轴不重合的直线 ,使得
,使得 ?并说明理由.
?并说明理由.
对于给定数列 ,如果存在实常数
,如果存在实常数 ,使得
,使得 对于任意的
对于任意的 都成立,我们称这个数列
都成立,我们称这个数列 是“
是“ 类数列”.
类数列”.
(1)若 ,判断数列
,判断数列 是否为“
是否为“ 类数列”,并说明理由;
类数列”,并说明理由;
(2)若数列 是“
是“ 类数列”,则数列
类数列”,则数列 、
、 是否一定是“
是否一定是“ 类数列”,若是的,加以证明;若不是,说明理由;
类数列”,若是的,加以证明;若不是,说明理由;
(3)若数列 满足:
满足: ,设数列
,设数列 的前
的前 项和为
项和为 ,求
,求 的表达式,并判断
的表达式,并判断 是否是“
是否是“ 类数列”.
类数列”.