对于给定数列 ,如果存在实常数
,如果存在实常数 ,使得
,使得 对于任意的
对于任意的 都成立,我们称这个数列
都成立,我们称这个数列 是“
是“ 类数列”.
类数列”.
(1)若 ,判断数列
,判断数列 是否为“
是否为“ 类数列”,并说明理由;
类数列”,并说明理由;
(2)若数列 是“
是“ 类数列”,则数列
类数列”,则数列 、
、 是否一定是“
是否一定是“ 类数列”,若是的,加以证明;若不是,说明理由;
类数列”,若是的,加以证明;若不是,说明理由;
(3)若数列 满足:
满足: ,设数列
,设数列 的前
的前 项和为
项和为 ,求
,求 的表达式,并判断
的表达式,并判断 是否是“
是否是“ 类数列”.
类数列”.
(附加题)将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落过程中,将3次遇到黑色障碍物,最后落入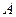 袋或
袋或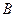 袋中.已知小球每次遇到黑色障碍物时向左、右两边下落的概率都是.
袋中.已知小球每次遇到黑色障碍物时向左、右两边下落的概率都是.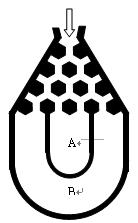
(Ⅰ)求小球落入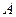 袋中的概率
袋中的概率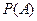 ;
;
(Ⅱ)在容器入口处依次放入4个小球,记X为落入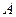 袋中小球的个数,试求X=3的概率和X的数学期望
袋中小球的个数,试求X=3的概率和X的数学期望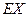 .
.
(15分)某地位于甲、乙两条河流的交汇处,根据统计资料预测,今年汛期甲河流发生洪水的概率为0.25,乙河流发生洪水的概率为0.18(假设两河流发生洪水与否互不影响).现有一台大型设备正在该地工作,为了保护设备,施工部门提出以下三种方案:
方案1:运走设备,此时需花费4000元;
方案2:建一保护围墙,需花费1000元,但围墙只能抵御一个河流发生的洪水,当两河流同时发生洪水时,设备仍将受损,损失约56 000元;
方案3:不采取措施,此时,当两河流都发生洪水时损失达60000元,只有一条河流发生洪水时,损失为10000元.
(1)试求方案3中损失费X(随机变量)的分布列;
(2)试比较哪一种方案好.
(13分)某篮球队与其他6支篮球队依次进行6场比赛,每场均决出胜负,设这支篮球队与其他篮球队比赛中获胜的事件是独立的,并且获胜的概率均为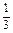 .
.
(1)求这支篮球队首次获胜前已经负了两场的概率;
(2)求这支篮球队在6场比赛中恰好获胜3场的概率;
(3)求这支篮球队在6场比赛中获胜场数的期望.
(12分)从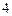 名男同学中选出
名男同学中选出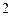 人,
人,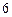 名女同学中选出
名女同学中选出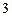 人,并将选出的
人,并将选出的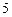 人排成一排.
人排成一排.
(1)共有多少种不同的排法?
(2)若选出的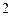 名男同学不相邻,共有多少种不同的排法?(用数字表示)
名男同学不相邻,共有多少种不同的排法?(用数字表示)
(本大题满分14分)
如图,已知直线L: 过椭圆C:
过椭圆C: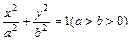 的右焦点F,
的右焦点F,
且交椭圆C于A、B两点,点A、B在直线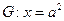 上的射影依次为点D、E.
上的射影依次为点D、E.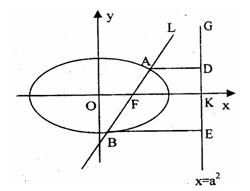
(Ⅰ)若抛物线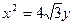 的焦点为椭圆C的上顶点,求椭圆C的方程;
的焦点为椭圆C的上顶点,求椭圆C的方程;
(Ⅱ)若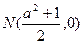 为x轴上一点;
为x轴上一点;
求证: A、N、E三点共线.