数列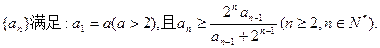
(1)求证: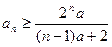 ;
;
(2)求证: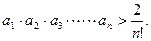

已知椭圆 的对称点落在直线
的对称点落在直线 )上,且椭圆C的离心率为
)上,且椭圆C的离心率为
(1)求椭圆C的方程;
(2)设A(3,0),M、N是椭圆C上关于x轴对称的任意两点,连结AN交椭圆于另一点E,求证直线ME与x轴相交于定点.
某企业准备投产一种新产品,经测算,已知每年生产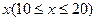 万件的该种产品所需要的总成本为
万件的该种产品所需要的总成本为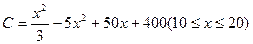 万元,市场销售情况可能出现好、中、差三种情况,各种情况发生的概率和相应的价格p(元)与年产量x之间的函数关系如下表所示.
万元,市场销售情况可能出现好、中、差三种情况,各种情况发生的概率和相应的价格p(元)与年产量x之间的函数关系如下表所示.
| 市场情况 |
概率 |
价格p与产量x的函数关系式 |
| 好 |
0.3 |
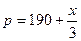 |
| 中 |
0.5 |
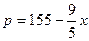 |
| 差 |
0.2 |
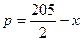 |
设L1、L2、L3分别表示市场情况好、中、差时的利润,随机变量ξx表示当年产量为x而市场情况不确定时的利润.
(1)分别求利润L1、L2、L3与年产量x之间的函数关系式;
(2)当产量x确定时,求随机变量ξx的期望Eξx;
(3)求年产量x为何值时,随机变量ξx的期望Eξx取得最大值(不需求最大值).
如图所示,已知四棱锥S—ABCD的底面ABCD是矩形,M、N分别是CD、SC的中点,SA⊥底面ABCD,SA=AD=1,AB= .
.
(1)求证:MN⊥平面ABN;
(2)求二面角A—BN—C的余弦值.
|
向量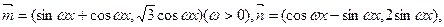 函数
函数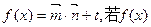 图象上相邻两个对称轴间的距离为
图象上相邻两个对称轴间的距离为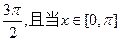 时,函数
时,函数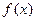 的最小值为0.
的最小值为0.
(1)求函数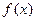 的表达式;
的表达式;
(2)在△ABC中,若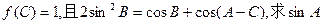 的值.
的值.