为了抓住世界杯商机,某商店决定购进A、B两种世界杯纪念品.若购进A种纪念品10件,B种纪念品5件,需要1 000元;若购进A种纪念品5件,B种纪念品3件,需要550元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定拿出1万元全部用来购进这两种纪念品,考虑市场需求,要求购进A种纪念品的数量不少于B种纪念品数量的6倍,且不超过B种纪念品数量的8倍,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
解方程:
求不等式 ≥
≥ 的负整数解。
的负整数解。
如图,四种图形各是哪种立体图形的表面展开所形成的?画出相应的四种立体图形.
在平面直角坐标系xOy中,二次函数y=mx2+(m﹣3)x﹣3(m>0)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
(1)求点A的坐标;
(2)当∠ABC=45°时,求m的值;
(3)已知一次函数y=kx+b,点P(n,0)是x轴上的一个动点,在(2)的条件下,过点P垂直于x轴的直线交这个一次函数的图象于点M,交二次函数y=mx2+(m﹣3)x﹣3(m>0)的图象于N.若只有当﹣2<n<2时,点M位于点N的上方,求这个一次函数的解析式.==
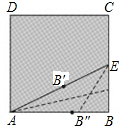
如图,用纸折出黄金分割点:裁一张正方的纸片ABCD,先折出BC的中点E,再折出线段AE,然后通过折叠使EB落到线段EA上,折出点B的新位置B′,因而EB′=EB.类似地,在AB上折出点B″使AB″=AB′.这时B″就是AB的黄金分割点.请你证明这个结论.