在一次购物抽奖活动中，假设某10张券中有一等奖券1张，可获价值50元的奖品；有二等奖券3张，每张可获价值10元的奖品；其余6张没有奖．某顾客从此10张奖券中任抽2张，求：
(1)该顾客中奖的概率；
(2)该顾客获得的奖品总价值
元的概率分布列．
（本小题满分14分）
已知函数
（1）若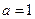
，点P为曲线
上的一个动点，求以点P为切点的切线斜率取最小值时的切线方程；
（2）若函数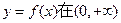
上为单调增函数，试求满足条件的最大整数a．
（本小题满分14分）如图，在四棱锥
中，底面
是边长为
的正方形，
、
分别为
、
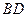的中点，侧面
，且
.
（1）求证：
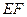∥平面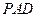
；（2）求三棱锥
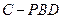的体积. 
（本小题满分12分）已知关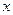
的一元二次函数
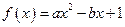，设集合
，分别从集合
和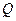
中随机取一个数
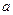和
得到数对
．（1）列举出所有的数对并求函数
有零点的概率；（2）求函数在区间
上是增函数的概率.
（本小题满分12分）已知函数
，求：
（1）函数
的最大值及取得最大值的自变量
的集合；（2）函数的单调增区间．
(本小题满分13分)
已知常数a为正实数，曲线Cn：y＝在其上一点Pn(xn，yn)的切线ln总经过定点(－a,0)(n∈N*).
(1)求证：点列：P1，P2，…，Pn在同一直线上；
(2)求证：
(n∈N*).