如图所示，直线AB为圆的切线，切点为B，点C在圆上，∠ABC的角平分线BE交圆于点E，DB垂直BE交圆于点D.
(1)证明：DB＝DC；
(2)设圆的半径为1，BC＝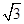
，延长CE交AB于点F，求△BCF外接圆的半径．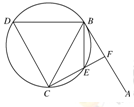
已知圆M过两点A(1，－1)，B(－1，1)，且圆心M在x＋y－2＝0上．
(1)求圆M的方程；
(2)设P是直线3x＋4y＋8＝0上的动点，PA′、PB′是圆M的两条切线，A′、B′为切点，求四边形PA′MB′面积的最小值．
如图，已知点A(－1，0)与点B(1，0)，C是圆x2＋y2＝1上的动点，连结BC并延长至D，使得CD＝BC，求AC与OD的交点P的轨迹方程．
P(x，y)在圆C：(x－1)2＋(y－1)2＝1上移动，试求x2＋y2的最小值．
如图，圆O1与圆O2的半径都是1，O1O2＝4，过动点P分别作圆O1、圆O2的切线PM、PN(M、N分别为切点)，使得PM＝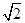
PN，试建立适当的坐标系，并求动点P的轨迹方程．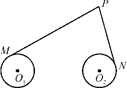
如图，已知直角坐标平面上点Q(2，0)和圆C：x2＋y2＝1，动点M到圆C的切线长与|MQ|的比等于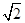
.求动点M的轨迹方程，并说明它表示什么．