对于函数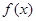 ,若存在实数对(
,若存在实数对(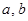 ),使得等式
),使得等式 对定义域中的每一个
对定义域中的每一个 都成立,则称函数
都成立,则称函数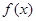 是“(
是“(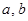 )型函数”.
)型函数”.
(1) 判断函数 是否为 “(
是否为 “(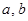 )型函数”,并说明理由;
)型函数”,并说明理由;
(2) 若函数 是“(
是“(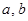 )型函数”,求出满足条件的一组实数对
)型函数”,求出满足条件的一组实数对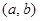 ;
;
(3)已知函数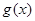 是“
是“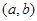 型函数”,对应的实数对
型函数”,对应的实数对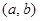 为
为 ,当
,当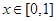 时,
时, ,若当
,若当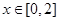 时,都有
时,都有 ,试求
,试求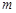 的取值范围.
的取值范围.
设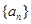 是等差数列,
是等差数列,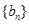 是各项都为正数的等比数列,且
是各项都为正数的等比数列,且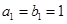 ,
,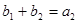 ,
, 。
。
(1)求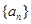 ,
,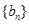 的通项公式;
的通项公式;
(2)求数列 的前n项和
的前n项和 .
.
如图,四边形ABCD为正方形,PD⊥平面ABCD ,PD∥QA,QA=AB=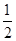 PD.
PD.
(1)证明:平面PQC⊥平面DCQ;
(2)求二面角Q—BP—C的正弦值.
在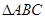 中,角
中,角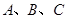 的对边分别为
的对边分别为 ,
,
且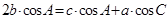 .
.
(1)求角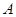 的大小;
的大小;
(2)若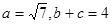 ,求
,求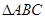 的面积
的面积
设函数

(Ⅰ)若 ,
,
( i )求 的值; (ii)在
的值; (ii)在 。
。
(Ⅱ)当
 上是单调函数,求
上是单调函数,求 的取值范围。(参考数据
的取值范围。(参考数据
如图所示,四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=1,E为BC的中点.
(1)求异面直线NE与AM所成角的余弦值;
(2)在线段AN上是否存在点S,使得ES⊥平面AMN?若存在,求线段AS的长;若不存在,请说明理由.