已知椭圆 的左、右顶点分别是
的左、右顶点分别是 、
、 ,左、右焦点分别是
,左、右焦点分别是 、
、 .若
.若 ,
, ,
, 成等比数列,求此椭圆的离心率.
成等比数列,求此椭圆的离心率.
在直角坐标系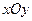 中,直线
中,直线 的参数方程为
的参数方程为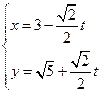 (
( 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系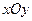 取相同的长度单位且以原点
取相同的长度单位且以原点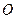 为极点,以
为极点,以 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆 的方程为
的方程为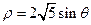 ,
,
(1)求圆 的直角坐标方程;
的直角坐标方程;
(2)设圆 与直线
与直线 交于点
交于点 、
、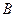 ,若
,若 的坐标为
的坐标为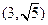 ,求
,求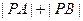 .
.
.已知 的展开式中,前三项的系数的绝对值依次成等差数列,
的展开式中,前三项的系数的绝对值依次成等差数列,
(1)证明:展开式中没有常数项;
(2)求展开式中所有有理项.
((本小题满分12分)
已知曲线C :
: (t为参数), C
(t为参数), C :
: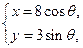
 (
( 为参数)。
为参数)。
(1)化C ,C
,C 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(2)若C 上的点P对应的参数为
上的点P对应的参数为 ,Q为C
,Q为C 上的动点,求
上的动点,求 中点
中点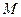 到直线
到直线 (t为参数)距离的最小值。
(t为参数)距离的最小值。
((本小题满分12分)
已知函数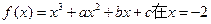 处取得极值,并且它的图象与直线
处取得极值,并且它的图象与直线 在点(1,0)处相切,(1)求
在点(1,0)处相切,(1)求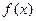 的解析式; (2)求
的解析式; (2)求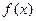 的单调区间.
的单调区间.
( (本题满分12分)
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.
| x |
3 |
4 |
5 |
6 |
| y |
2.5 |
3 |
4 |
4.5 |
(1)请根据上表提供的数据,求出 y关于x的线性回归方程
y关于x的线性回归方程
(2)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(1)求出的线性回归方程预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)
(参考公式: 回归直线的方程是
回归直线的方程是 ,
,
其中 ,
, ,)
,)