等边△ABC的边长为2，P是BC边上的任一点（与B、C不重合），连接AP，以AP为边向两侧作等边△APD和等边△APE，分别与边AB、AC交于点M、N（如图1）。
（1）求证：AM=AN；
（2）设BP=x。
①若，BM=
，求x的值；
②记四边形ADPE与△ABC重叠部分的面积为S，求S与x之间的函数关系式以及S的最小值；
③连接DE，分别与边AB、AC交于点G、H（如图2），当x取何值时，∠BAD=150？并判断此时以DG、GH、HE这三条线段为边构成的三角形是什么特殊三角形，请说明理由。
端午节期间，某食品店平均每天可卖出300只粽子，且卖出1只粽子的利润是1元。经调查发现，零售单价每降0．1元，每天可多卖出100只粽子。为了使每天获取的利润更多，该店决定把零售单价下降
元。在不考虑其他因素的条件下，当
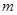定为多少时，才能使该店每天获取的利润是420元，并且卖出的粽子更多？
如图：已知二次函数的图象经过点A（－1，0），B（3，0），C（0，－5），
（1）试确定此二次函数的解析式；
（2）点P是抛物线对称轴上的一个动点,是否存在点P,使PB+PC的值最小,如果存在,请求出点P的坐标,如果不存在,请说明理由。
六一儿童节，某学习用品销售商店推出两种优惠方法：①购1个书包，赠送1支水性笔；②购书包和水性笔一律按9折优惠。其中，书包每个定价20元，水性笔每支定价5元。小丽和同学需买4个书包，水性笔若干支（不少于4支）。
（1）分别写出两种优惠方法购买费用
（元）与所买水性笔支数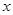
（支）的函数解析式（请化简函数解析式）；
（2）对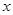的取值情况进行分析，说明按哪种优惠方法购买比较便宜。
如图，杂技团进行杂技表演，演员从跷跷板右端A处弹跳到人梯顶端椅子B处，其身体（看成一点）的路线是抛物线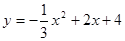
的一部分。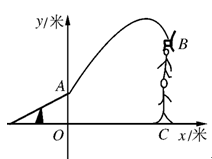
（1）求演员弹跳离地面的最大高度；
（2）已知在一次表演中，人梯高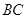
=4米，人梯到起跳点
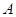的水平距离是6米，问这次表演是否成功？请说明理由。
经统计分析，南博会期间，昆明环湖东路上的车流速度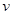
（千米／小时）是车流密度
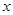（辆／千米）的一次函数。当车流密度为20辆／千米时，车流速度为80千米／小时；当车流密度达到220辆／千米时，造成堵塞，此时车流速度为0千米/小时。求大桥上车流密度为100辆／千米时的车流速度。