一列长110米的火车以每小时30千米的速度向北缓缓驶去,铁路旁一条小路上,一位工人也正向北步行。14时10分时火车追上这位工人,15秒后离开。14时16分迎面遇到一个向南走的学生,12秒后离开这个学生。问:工人与学生将在何时相遇?
数轴上A,B两点分别表示-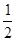 和
和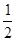 ,这两点间的点表示的有理数能有多少个?试写出其中五个。
,这两点间的点表示的有理数能有多少个?试写出其中五个。
画一条数轴,然后在数轴上画出表示下列各数的点;并比较大小。
-1 ,2, 3,-2.7,1
,2, 3,-2.7,1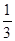 ,-3,0
,-3,0
如图,一只蚂蚁从原点O出发,它先向右爬了2个单位长度到达点A,再向右爬了3个单位长度到达点B,然后向左爬了9个单位长度到达点C。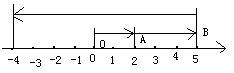
(1)写出A,B,C三点表示的数;
(2)根据C点在数轴上的位置回答蚂蚁实际上是从原点出发,向什么方向爬行了几个单位长度?
已知直线 与抛物线
与抛物线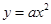 交于点A(1,
交于点A(1, ),与
),与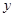 轴交于点C.
轴交于点C.
(1)求抛物线的解析式和点C的坐标;
(2)把(1)中的抛物线向右平移2个单位,再向上平移 个单位(
个单位( >0),抛物线与
>0),抛物线与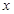 轴交于P、Q两点,过C、P、Q三点的圆恰好以CQ为直径,求
轴交于P、Q两点,过C、P、Q三点的圆恰好以CQ为直径,求 的值;
的值;
(3)如图,把抛物线向右平移2个单位,再向上平移 个单位(
个单位( >0),抛物线与
>0),抛物线与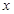 轴交于P、Q两点,过C、P、Q三点的圆的面积是否存在最小值?若存在,请求出这个最小值和此时
轴交于P、Q两点,过C、P、Q三点的圆的面积是否存在最小值?若存在,请求出这个最小值和此时 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.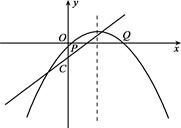
如图,已知函数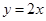 和函数
和函数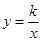 的图象交于A、B两点,过点A作AE⊥
的图象交于A、B两点,过点A作AE⊥ 轴于点E,若△AOE的面积为4.
轴于点E,若△AOE的面积为4.
(1)求反比例函数的解析式;
(2)求点A、B的坐标;
(3)P是坐标平面上的点,且以点B、A、E、P为顶点的四边形是平行四边形,直接写出满足条件的P点坐标.