某房屋开发公司用100万元购得一块土地,该地可以建造每层1000m2的楼房,楼房的总建筑面积(即各层面积之和)每平方米平均建筑费用与建筑高度有关,楼房每升高一层,整幢楼房每平方米建筑费用提高5%。已知建筑5层楼房时,每平方米建筑费用为400元,公司打算造一幢高于5层的楼房,为了使该楼房每平方和的平均综合费用最低(综合费用是建筑费用与购地费用之和),公司应把楼层建成几层?
选修4—5: 不等式选讲.
(Ⅰ)设函数 .证明:
.证明: ;
;
(Ⅱ)若实数 满足
满足 ,求证:
,求证:
选修4—4:坐标系与参数方程.
坐标系与参数方程在直角坐标系xOy中,圆C的参数方程 为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
(Ⅰ)求圆C的极坐标方程;
(Ⅱ)射线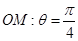 与圆C的交点为O、P两点,求P点的极坐标.
与圆C的交点为O、P两点,求P点的极坐标.
选修4—1:几何证明选讲.
已知圆内接△ABC中,D为BC上一点,且△ADC为正三角形,点E为BC的延长线上一点,AE为圆O的切线.
(Ⅰ)求∠BAE 的度数;
(Ⅱ)求证:
设函数
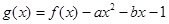 ,其中
,其中 为自然对数的底数.
为自然对数的底数.
(Ⅰ)已知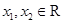 ,求证:
,求证: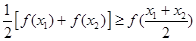 ;
;
(Ⅱ)函数 是
是 的导函数,求函数
的导函数,求函数 在区间
在区间 上的最小值.
上的最小值.
设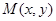 到定点
到定点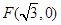 的距离和它到直线
的距离和它到直线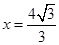 距离的比是
距离的比是 .
.
(Ⅰ)求点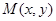 的轨迹方程;
的轨迹方程;
(Ⅱ) 为坐标原点,斜率为
为坐标原点,斜率为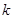 的直线过
的直线过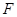 点,且与点
点,且与点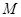 的轨迹交于点
的轨迹交于点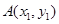 ,
,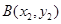 ,若
,若 ,求△
,求△ 的面积.
的面积.