选修4—4:坐标系与参数方程.
坐标系与参数方程在直角坐标系xOy中,圆C的参数方程 为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
(Ⅰ)求圆C的极坐标方程;
(Ⅱ)射线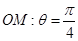 与圆C的交点为O、P两点,求P点的极坐标.
与圆C的交点为O、P两点,求P点的极坐标.
如图,正方形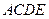 与等腰直角△ACB所在的平面互相垂直,且AC=BC=2,
与等腰直角△ACB所在的平面互相垂直,且AC=BC=2,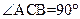 , F、G分别是线段AE、BC的中点.求
, F、G分别是线段AE、BC的中点.求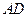 与
与 所成的角的余弦值.
所成的角的余弦值.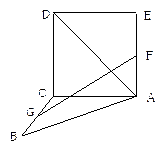
已知函数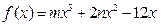 的减区间是
的减区间是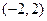 .
.
⑴试求m、n的值;
⑵求过点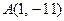 且与曲线
且与曲线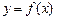 相切的切线方程;
相切的切线方程;
⑶过点A(1,t)是否存在与曲线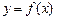 相切的3条切线,若存在求实数t的取值范围;若不存在,请说明理由.
相切的3条切线,若存在求实数t的取值范围;若不存在,请说明理由.
设椭圆M: (a>b>0)的离心率与双曲线
(a>b>0)的离心率与双曲线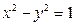 的离心率互为倒数,且内切于圆
的离心率互为倒数,且内切于圆 .
.
(1)求椭圆M的方程;
(2)若直线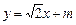 交椭圆于A、B两点,椭圆上一点
交椭圆于A、B两点,椭圆上一点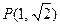 ,
,
求△PAB面积的最大值.
如图,在六面体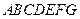 中,平面
中,平面 ∥平面
∥平面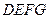 ,
,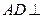 平面
平面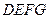 ,
, ,
, ,
,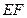 ∥
∥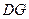 ,且
,且 ,
, .
.
(1)求证:平面 平面
平面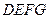 ;
;
(2)求证: ∥平面
∥平面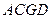 ;
;
(3)求三棱锥 的体积.
的体积.
某学校共有教职工900人,分成三个批次进行继续教育培训,在三个批次中男、女教职工人数如表. 已知在全体教职工中随机抽取1名,抽到第二批次中女教职工的概率是0.16
| 第一批次 |
第二批次 |
第三批次 |
|
| 女教职工 |
196 |
x |
y |
| 男教职工 |
204 |
156 |
z |
(1)求 的值;
的值;
(2)现用分层抽样的方法在全体教职工中抽取54名做培训效果的调查, 问应在第三批次中
抽取教职工多少名?
(3)已知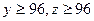 ,求第三批次中女教职工比男教职工多的概率.
,求第三批次中女教职工比男教职工多的概率.