如图所示，重量为G＝10N的木块静止在倾角为37°的固定斜面上，木块与斜面间的动摩擦因素μ=0.8。已知木块与斜面间的最大静摩擦力近似等于滑动摩擦力，重力加速度g=10m/s2，sin37° =0.6，cos37° =0.8，求：
（1）.斜面对木块的支持力大小N
（2）木块对斜面的的摩擦力大小f和方向
（3）若对木块施加一个平行斜面向上的拉力，拉力大小F=13N，求此时斜面对木块的摩擦力大小f ‘ 和方向.
(15分)如图所示，在宽度为L的两虚线区域内存在匀强电场，一质量为m，带电量为＋q的滑块(可看成点电荷)，从距该区域为L的绝缘水平面上以初速度v0向右运动并进入电场区域，滑块与水平面间的动摩擦因数为μ。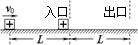
⑴若该区域电场为水平方向，并且用速度传感器测得滑块从出口处滑出的速度与进入该区域的速度相同，求该区域的电场强度大小与方向，以及滑块滑出该区域的速度；
⑵若该区域电场为水平方向，并且用速度传感器测得滑块滑出该区域的速度等于滑块的初速度v0，求该区域的电场强度大小与方向；
⑶若将该区域电场改为竖直方向，测出滑块到达出口处速度为v0/2(此问中取v0＝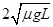
)，再将该区域电场反向后，发现滑块未能从出口滑出，求滑块所停位置距左边界多远。
(14分)某同学玩“弹珠游戏”装置如图所示，S形管道BC由两个半径为R的1/4圆形管道拼接而成，管道内直径略大于小球直径，且远小于R，忽略一切摩擦，用质量为m的小球将弹簧压缩到A位置，由静止释放，小球到达管道最高点C时对管道恰好无作用力，求：( )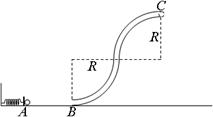
⑴小球到达最高点C的速度大小；
⑵若改用同样大小质量为2m的小球做游戏，其它条件不变，求小球能到达的最大高度；
⑶若改用同样大小质量为m/4的小球做游戏，其它条件不变，求小球落地点到B点的距离。
(10分)如图所示，质量为60kg的滑雪运动员，在倾角θ为37°的斜坡顶端，从静止开始自由下滑50m到达坡底，用时5s，然后沿着水平路面继续自由滑行，直至停止，不计拐角处能量损失，滑板与斜面及水平面间的动摩擦因数相同，g取10m/s2，sin37°＝0.6，cos37°＝0.8，求：( )
⑴运动员下滑过程中的加速度大小；
⑵滑板与坡面间的滑动摩擦力大小；
⑶运动员在水平路面上滑行的时间。
甲车在前以10m/s的速度匀速行驶，乙车在后以6m/s的速度行驶．当两车相距12m时，甲车开始刹车，加速度大小为2m/s2，问：
（1）经过多长时间两车间距离最大？
（2）他们间的最大距离为多少？
（3）经多少时间乙车可追上甲车？
如图所示，一倾角为30°的光滑斜面与水平地面平滑连接，水平地面的动摩擦因数为0.25，前方距离斜面底端B点10m处有一个障碍物Q。现有一小孩从斜面上h=3m高处的A点由静止开始滑下，不计小孩到斜面底端时受到的冲击（即到达B点前后瞬间速度大小不变），取g=10m/s2，试回答下列问题：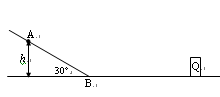
（1）小孩到达斜面底端时的速度大小是多少？
（2）试通过计算判断，小孩会不会碰到障碍物？
（3）接上述第（2）问，若不碰到障碍物，则小孩停在水平面上的位置距离障碍物有多远？若会碰到障碍物，则为了安全，小孩从斜面上静止开始下滑的高度不得超过多少？