下列说法正确的是( )
| A.有公共顶点的两个角是对顶角 |
| B.有公共顶点并且相等的两个角是对顶角 |
| C.两条直线相交所得的四个角中的任意两个角,不是邻补角,就是对顶角 |
| D.相等的两个角一定是对顶角 |
如图,直线a,b相交于点O,若∠1等于40°,则∠2等于( )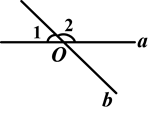
| A.50° |
| B.60° |
| C.140° |
| D.160° |
邻补角是指( )
| A.和为180°的两个角 |
| B.有公共顶点且互补的两个角 |
| C.有一条公共边且相等的两个角 |
| D.有公共顶点且有一条公共边,另一边互为反向延长线的两个角 |
下面四个图形中,∠1与∠2是邻补角的是( )
A. |
B. |
C.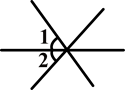 |
D. |
下列图形中∠1与∠2是对顶角的图形共有( )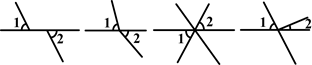
| A.0个 |
| B.1个 |
| C.2个 |
| D.3个 |