如图所示,两平行导轨间距L=0.1 m,足够长光滑的倾斜部分和粗糙的水平部分圆滑连接,倾斜部分与水平面的夹角θ=30°,垂直斜面方向向上的磁场磁感应强度B=0.5 T,水平部分没有磁场.金属棒ab质量m=0.005 kg、电阻r=0.02 Ω,运动中与导轨始终接触良好,并且垂直于导轨.电阻R=0.08 Ω,其余电阻不计.当金属棒从斜面上离地高h=1.0 m以上的任何地方由静止释放后,在水平面上滑行的最大距离x都是1.25 m.取g=10 m/s2,求: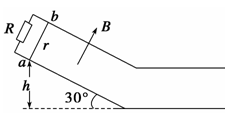
(1)金属棒在斜面上的最大速度;
(2)金属棒与水平面间的动摩擦因数;
(3)从高度h=1.0 m处滑下后电阻R上产生的热量.
“加速度计”作为测定运动物体加速度的仪器,已被广泛应用,图甲所示为应变式加速度计的原理图:支架AB固定在待测系统上,滑块穿在AB之间的水平光滑杆上,并用轻弹簧连接在A端,其下端有一活动臂可在滑动变阻器上自由滑动.随着系统沿水平方向做变速运动,滑块相对于支架将发生位移,并通过电路转换成电信号从电压表输出.已知电压表量程为8V,滑块质量m=0.1kg,弹簧劲度系数k=20N/m,电源电动势E=10V,内阻不计,滑动变阻器总电阻值R=40Ω,有效总长度l=8cm.当待测系统静上时,滑动触头P位于变阻器R的中点,取A→B方向为速度正方向。
(1)确定该加速度计测量加速度的范围。
(2)为保证电压表能正常使用,图甲电路中电阻R0至少应为多大?
(3)根据R0的最小值,写出待测系统沿A→B做变速运动时,电压表输出电压UV与加速度a的关系式.
(4)根据R0的最小值,将电压表盘上的电压刻度改成适当的加速度刻度,将对应的加速度值填入图乙中电压表盘的小圆内。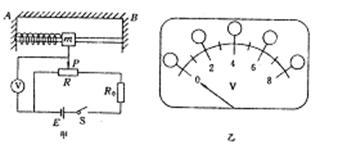
A、B分别为竖直固定光滑圆轨道的最低点和最高点。已知小球通过A点的速率为2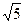 m/s,试求它通过B点速率的最小值。
m/s,试求它通过B点速率的最小值。
如图13所示,水上滑梯由斜槽AB和水平槽BC构成,AB与BC圆滑连接,斜槽的竖直高度 ,BC面高出水面的距离
,BC面高出水面的距离 。一质量m=50kg的游戏者从滑梯顶端A
。一质量m=50kg的游戏者从滑梯顶端A 点由静止滑下,
点由静止滑下, 取10mol/s2。
取10mol/s2。
(1)若忽略游戏者下滑过程中受到的一切阻力,求游戏者从斜槽顶端A点由静止滑下到斜槽底端B点的速度大小;
(2)若由于阻力的作用,游戏者从滑梯顶端A点由静止滑下到达滑梯末端C点时的速度大小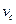 =15m/s,求这一过程中游戏者克服阻力做的功;
=15m/s,求这一过程中游戏者克服阻力做的功;
(3)若游戏者滑到滑梯末端C点以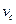 =15m/s的速度水平飞出,求他从C点水平飞出到落入水中时,他在空中运动过程中水平方向的位移。
=15m/s的速度水平飞出,求他从C点水平飞出到落入水中时,他在空中运动过程中水平方向的位移。
如图15所示,固定在上、下两层水平面上的平行金属导轨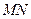 、
、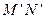 和
和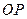 、
、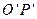 间距都是
间距都是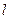 ,二者之间固定有两组竖直半圆形轨道
,二者之间固定有两组竖直半圆形轨道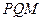 和
和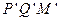 ,两轨道间距也均为
,两轨道间距也均为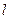 ,且
,且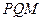 和
和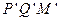 的竖直高度均为4R,两组半圆形轨道的半径均为R。轨道的
的竖直高度均为4R,两组半圆形轨道的半径均为R。轨道的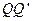 端、
端、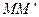 端的对接狭缝宽度可忽略不计,图中的虚线为绝缘材料制成的固定支架,能使导轨系统位置固定。将一质量为
端的对接狭缝宽度可忽略不计,图中的虚线为绝缘材料制成的固定支架,能使导轨系统位置固定。将一质量为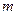 的金属杆沿垂直导轨方向放在下层导轨的最左端
的金属杆沿垂直导轨方向放在下层导轨的最左端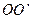 位置,金属杆在与水平成
位置,金属杆在与水平成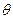 角斜向上的恒力作用下沿导轨运动,运动过程中金属杆始终与导轨垂直,且接触良好。当金属杆通过4R的距离运动到导轨末端
角斜向上的恒力作用下沿导轨运动,运动过程中金属杆始终与导轨垂直,且接触良好。当金属杆通过4R的距离运动到导轨末端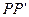 位置时其速度大小
位置时其速度大小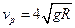 。金属杆和导轨的电阻、金属杆在半圆轨道和上层水平导轨上运动过程中所受的摩擦阻力,以及整个运动过程中所受空气阻力均可忽略不计。
。金属杆和导轨的电阻、金属杆在半圆轨道和上层水平导轨上运动过程中所受的摩擦阻力,以及整个运动过程中所受空气阻力均可忽略不计。
(1)已知金属杆与下层导轨间的动摩擦因数为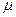 ,求金属杆所受恒力F的大小;
,求金属杆所受恒力F的大小;
(2)金属杆运动到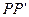 位置时撤去恒力F,金属杆将无碰撞地水平进入第一组半圆轨道
位置时撤去恒力F,金属杆将无碰撞地水平进入第一组半圆轨道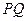 和
和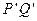 ,又在对接狭缝
,又在对接狭缝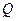 和
和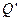 处无碰撞地水平进入第二组半圆形轨道
处无碰撞地水平进入第二组半圆形轨道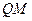 和
和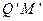 的内侧,求金属杆运动到半圆轨道的最高位置
的内侧,求金属杆运动到半圆轨道的最高位置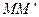 时,它对轨道作用力的大小;
时,它对轨道作用力的大小;
(3)若上层水平导轨足够长,其右端连接的定值电阻阻值为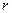 ,导轨处于磁感应强度为B、方向竖直向下的匀强磁场中。金属杆由第二组半圆轨道的最高位置
,导轨处于磁感应强度为B、方向竖直向下的匀强磁场中。金属杆由第二组半圆轨道的最高位置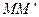 处,无碰撞地水平进入上层导轨后,能沿上层导轨滑行。求金属杆在上层导轨上滑行的最大距离。
处,无碰撞地水平进入上层导轨后,能沿上层导轨滑行。求金属杆在上层导轨上滑行的最大距离。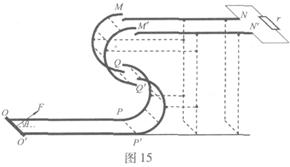
示波管是示波器的核心部分,它主要由电子枪、偏转系统和荧光屏三部分组成,如图14甲所示。电子枪具有释放电子并使电子聚集成束以及加速的作用;偏转系统使电子束发生偏转;电子束打在荧光屏上形成光迹。这三部分均封装于真空玻璃壳中。已知电子的电荷量 =1.6×10
=1.6×10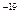 C,质量
C,质量 =0.91×10
=0.91×10 kg,电子所受重力及电子之间的相互作用力均可忽略不计,不考虑相对论效应。
kg,电子所受重力及电子之间的相互作用力均可忽略不计,不考虑相对论效应。 (1)电子枪的三级加速可简化为如图14乙所示的加速电场,若从阴极逸出电子的初速度可忽略不计,要使电子被加速后的动能达到16×10
(1)电子枪的三级加速可简化为如图14乙所示的加速电场,若从阴极逸出电子的初速度可忽略不计,要使电子被加速后的动能达到16×10 J,求加速电压
J,求加速电压 为多大;
为多大;
(2)电子被加速后进入偏转系统,若只考虑电子沿Y(竖直)方向的偏转情况,偏转系统可以简化为如图14丙所示的偏转电场。偏转电极的极板长 =4.0cm,两板间距离
=4.0cm,两板间距离 =1.0cm,极板右端与荧光屏的距离
=1.0cm,极板右端与荧光屏的距离 =18cm,当在偏转电极上加
=18cm,当在偏转电极上加 的正弦交变电压时,如果电子进入偏转电场的初速度
的正弦交变电压时,如果电子进入偏转电场的初速度 ,求电子打在荧光屏上产生亮线的最大长度;
,求电子打在荧光屏上产生亮线的最大长度;
(3)如图14甲所示,电子枪中灯丝用来加热阴极,使阴极发射电子。控制栅极的电势比阴极的电势低,调节阴极与控制栅极之间的电压,可控制通过栅极电子的数量。现要使打在荧光屏上电子的数量增加,应如何调节阴极与控制栅极之间的电压。电子枪中 、
、 和
和 三个阳极除了对电子加速外,还共同完成对电子的聚焦作用,其中聚焦电场可简化为如图14丁所示的电场,图中的虚线是该电场的等势线。请简要说明聚焦电场如何实现对电子的聚焦作用。
三个阳极除了对电子加速外,还共同完成对电子的聚焦作用,其中聚焦电场可简化为如图14丁所示的电场,图中的虚线是该电场的等势线。请简要说明聚焦电场如何实现对电子的聚焦作用。