下表是淮河某河段今年雨季一周内水位变化情况,(其中0表示警戒水位)那么水位最高是( )
| 星期 |
一 |
二 |
三 |
四 |
五 |
六 |
日 |
| 水位变化/米 |
+0.03 |
+0.41 |
+0.25 |
+0.10 |
0 |
-0.13 |
-0.2 |
A.周一 B.周二 C.周三 D.周五
下列四个函数图象中,当x>0时,y随x的增大而减小的是(). 
股票每天的涨、跌幅均不能超过10%,即当涨了原价的10%后,便不能再涨,叫做涨停;当跌了原价的10%后,便不能再跌,叫做跌停.已知一支股票某天跌停,之后两天时间又涨回到原价,若这两天此股票股价的平均增长率为x,则x满足的方程是().
| A. |
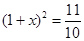
|
B. |
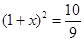
|
| C. |

|
D. |
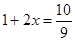
|
学校要组织足球比赛,赛制为单循环形式(每两队之间赛一场),计划安排21场比赛,应邀请多少个球队参赛?设邀请x个球队参赛,根据题意,下面所列方程正确的是().
| A. |
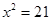
|
B. |
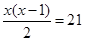
|
C. |
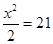
|
D. |
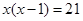
|
对二次函数y= -(x+2) 2-3,描述错误的是().
| A. | 图象开口向下 | B. | 关于直线x=2对称 |
| C. | 函数有最大值为-3 | D. | 图象与x轴无交点 |
已知x 2+y 2-4x+6y+13=0,则代数式x+y的值为().
| A. | -1 | B. | 1 | C. | 5 | D. | 36 |