如图，在△ABC中，∠B=90°，AB=6cm，BC=8cm，点P、Q为AB边及BC边上的两个动点。（1）若点P从点A沿AB边向点B以1cm/s的速度移动，与此同时，点Q从点B开始沿BC边向点C以2cm/s的速度移动，两个点同时出发。
①经过几秒，△PBQ的面积等于8cm2；
②是否存在这样的时刻，使△PBQ的面积等于10 cm2？如果存在请求出来，如果不存在，请说明理由。
（2）假设点P、Q可以分别在AB、BC边上任意移动，是否存在PQ同时平分△ABC的周长和面积的情况？如果存在请求出BP的长度；如果不存在，请说明理由。
如图，矩形ABCD的对角线AC、BD相交于点O，DE∥AC，CE∥BD.
（1）求证：四边形OCED为菱形；
（2）连接AE、BE，AE与BE相等吗？请说明理由.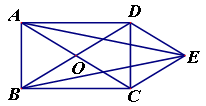
我市启动了第二届“美丽港城·美在悦读”全民阅读活动。为了了解市民每天的阅读时间情况，随机抽取了部分民进行调查。根据调查结果绘制如下尚不完整的频数分布表：
| 阅读时间 x（min） |
0≤x<30 |
30≤x<60 |
60≤x<90 |
x≥90 |
合计 |
| 频数 |
450 |
400 |
50 |
||
| 频率 |
0．4 |
0．1 |
1 |
（1）补全表格：
（2）将每天阅读时间不低于60min的市民称为“阅读爱好者”。若我市约有500万人，请估计我市能称为“阅读爱好者”的市民有多少万人？
解分式方程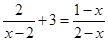 
.
解不等式2(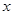
–1)+5<3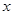，并把解集在数轴上表示出来.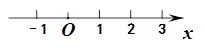 
如图，抛物线y=ax2+bx+c（a≠0）与x轴交于A（﹣1，0），B（4，0）两点，与y轴交于点C（0，2），点M（m，n）是抛物线上一动点，位于对称轴的左侧，并且不在坐标轴上，过点M作x轴的平行线交y轴于点Q，交抛物线于另一点E，直线BM交y轴于点F．
（1）求抛物线的解析式，并写出其顶点坐标；
（2）当S△MFQ：S△MEB=1：3时，求点M的坐标．