【问题情境】已知矩形的面积为a（a为常数，a＞0），当该矩形的长为多少时，它的周长最小？最小值是多少？
【数学模型】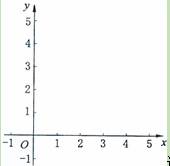
设该矩形的长为x，周长为y，则y与x的函数关系式为y=2（x+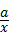
）（x＞0）．
【探索研究】（1）我们可以借鉴以前研究函数的经验，先探索函数y=x+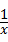
（x＞0）的图象和性质．
①填写下表，画出函数的图象；
| x |
… |
 |
 |
 |
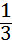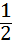1 |
2 |
3 |
4 |
… |
| y |
… |
|
|
|
|
|
|
|
… |
②观察图象，写出该函数两条不同类型的性质；
③在求二次函数y=ax2+bx+c（a≠0）的最大（小）值时，除了通过观察图象，还可以通过配方得到．请你通过配方求函数y=x+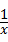（x＞0）的最小值
【解决问题】
（2）用上述方法解决“问题情境”中的问题，直接写出答案．
解方程：（每小题4分，共8分）
（1）
；
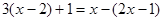（2）
．
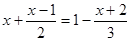如图，△ABC中，∠ACB=90°，AB=5cm，BC=3cm，若点P从点A出发，以每秒2cm的速度沿折线A—C—B向点B运动，设运动时间为t秒（t>0），
（1）在AC上是否存在点P使得PA=PB？若存在，求出t的值；若不存在，说明理由；
（2）若点P恰好在△ABC的角平分线上，请直接写出t的值．
如图，已知直线l1∥l2∥l3，且l1，l2之间的距离为1， l2，l3之间的距离为2 ，点A、C分别在直线l2，l1上，
（1）利用直尺和圆规作出以AC为底的等腰△ABC，使得点B落在直线l3上（保留作图痕迹，不写作法）；
（2）若（1）中得到的△ABC为等腰直角三角形，求AC的长．
如图，△
是等边三角形，点
、
分别是
、
的延长线上的点，且
，
的延长线交
于点
．
（1）求证：
；
（2）求
的度数．
如图，在等腰RT△
中，
，
，点
是斜边
的中点，点
、
分别为
、
边上的点，且
．
（1）判断
与
的大小关系，并说明理由；
（2）若
，
，求△
的面积．