在等边三角形ABC中,AD⊥BC于点D.
(1)如图1,请你直接写出线段AD与BC之间的数量关系: AD= BC ;
(2)如图2,若P是线段BC上一个动点(点P不与点B、C重合),联结AP,将线段AP绕点A逆时针旋转60°,得到线段AE,联结CE,猜想线段AD、CE、PC之间的数量关系,并证明你的结论;
(3)如图3,若点P是线段BC延长线上一个动点,(2)中的其他条件不变,按照(2)中的作法,请在图3中补全图形,并直接写出线段AD、CE、PC之间的数量关系.
(本题6分) 如图,已知∠1+∠2=180°,∠DEF=∠A,试判断∠ACB与∠DEB的大小关系,
并对结论进行说明.
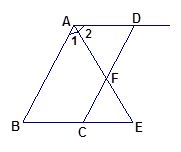
(本题6分) 如图,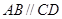 ,
,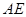 平分
平分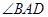 ,
,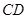 与
与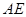 相交于点
相交于点 ,
,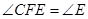 。试说明:
。试说明: 。
。
如图,已知: ,
,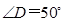 ,求
,求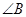 的度数。
的度数。
根据题意填空(本题5分)
已知,如图,AD∥BC,∠BAD=∠BCD,
求证:AB∥CD.
证明:∵AD∥BC(已知)
∴∠1=( )
又∵∠BAD=∠BCD ( 已知 )
∴∠BAD-∠1=∠BCD-∠2( )
即:∠3=∠4
∴( )
观察等式: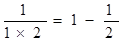 ,
,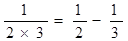 ,
, ,
,
将以上三个等式两边分别相加得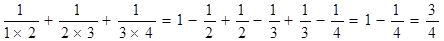 .
.
(1)猜想并写出: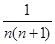 =____________________.
=____________________.
(2)直接写出下式的计算结果: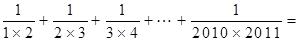 __________________________.
__________________________.
(3)探究并计算: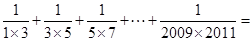 ______________________.
______________________.