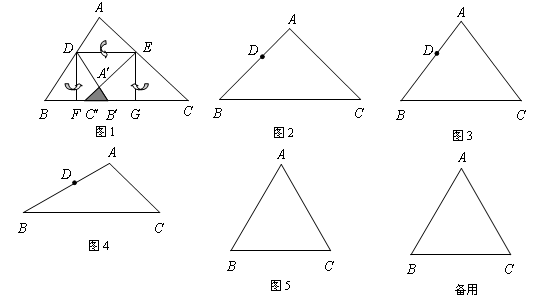
如图1，已知有一张三角形纸片ABC的一边AB=10，若D为AB边上的点，过点D作DE∥BC交AC于点E，分别过点D、E作DF⊥BC于F，EG⊥BC于G，把三角形纸片ABC分别沿DE、DF、EG按图1方式折叠，点A、B、C分别落在A′、B′、C′处．若点A′、B′、C′在矩形DFGE内或者其边上，且互不重合，此时我们称△A′B′C′（即图中阴影部分）为“重叠三角形”．
实践探究：
（1）当AD=4时，
①若∠A=90°，AB=AC，请在图2中画出“重叠三角形”，S△A′B′C′= ；
②若AB=AC，BC=12，如图3，S△A′B′C′= ；
③若∠B=30°，∠C=45°，如图4，S△A′B′C′= .
（2）若△ABC为等边三角形（如图5），AD=m，且重叠三角形A′B′C′存在，试用含m的代数式表示重叠三角形A′B′C′ 的面积，并写出m的取值范围.
甲、乙二人在一环形场地上从A点同时同向匀速跑步，甲的速度是乙的2.5倍，4分钟两人首次相遇，此时乙还需要跑300米才跑完第一圈，求甲、乙二人的速度及环形场地的周长．（列方程（ 组） 求解）
在
ABCD中，点E、F分别在AB、CD上，且AE=CF．
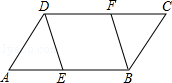
（1）求证：△ADE≌△CBF；
（2）若DF=BF，求证：四边形DEBF为菱形．
先化简，再求值：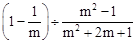
，其中m=2．
问题探究
（1）请在图①中作出两条直线，使它们将圆面四等分；
（2）如图②，M是正方形ABCD内一定点，请在图②中作出两条直线（要求其中一条直线必须过点M），使它们将正方形ABCD的面积四等分，并说明理由.
问题解决
（3）如图③，在四边形ABCD中，AB∥CD，AB+CD=BC，点P是AD的中点，如果AB=
，CD=
，且
，那么在边BC上是否存在一点Q，使PQ所在直线将四边形ABCD的面积分成相等的两部分？若存在，求出BQ的长；若不存在，说明理由.
在平面直角坐标系中，一个二次函数的图象经过点A（1，0）、B（3，0）两点．
（1）写出这个二次函数的对称轴；
（2）设这个二次函数的顶点为D，与y轴交于点C，它的对称轴与x轴交于点E，连接AD、DE和DB，当△AOC与△DEB相似时，求这个二次函数的表达式。
[提示：如果一个二次函数的图象与x轴的交点为
A，那么它的表达式可表示为：
]