已知不等式 .
.
(1)求该不等式的解集M;
(2)若 ,求证:
,求证:
已知M(-3,0)﹑N(3,0),P为坐标平面上的动点,且直线PM与直线PN的斜率之积为常数m(m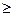 -1,m
-1,m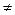 0).
0).
(1)求P点的轨迹方程并讨论轨迹是什么曲线?
(2)若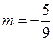 , P点的轨迹为曲线C,过点Q(2,0)斜率为
, P点的轨迹为曲线C,过点Q(2,0)斜率为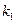 的直线
的直线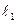 与曲线C交于不同的两点A﹑B,AB中点为R,直线OR(O为坐标原点)的斜率为
与曲线C交于不同的两点A﹑B,AB中点为R,直线OR(O为坐标原点)的斜率为 ,求证
,求证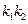 为定值;
为定值;
(3)在(2)的条件下,设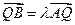 ,且
,且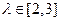 ,求
,求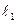 在y轴上的截距的变化范围.
在y轴上的截距的变化范围.
如图所示的几何体 中,
中,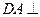 平面
平面 ,
,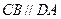 ,
,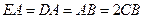 ,
,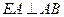 ,
,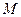 是
是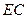 的中点。
的中点。
(Ⅰ)求证: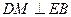 ;
;
(Ⅱ)设二面角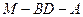 的平面角为
的平面角为 ,求
,求 。
。
已知点 是中心在原点,长轴在x轴上的椭圆的一个顶点,离心率为
是中心在原点,长轴在x轴上的椭圆的一个顶点,离心率为 ,
,
椭圆的左右焦点分别为F1和F2 。
(Ⅰ)求椭圆方程;
(Ⅱ)点M在椭圆上,求⊿MF1F2面积的最大值;
(Ⅲ)试探究椭圆上是否存在一点P,使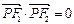 ,若存在,请求出点P的坐标;
,若存在,请求出点P的坐标;
若不存在,请说明理由。
在直角坐标系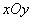 中,以
中,以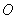 为圆心的圆与直线
为圆心的圆与直线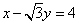 相切.
相切.
(1)求圆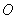 的方程;(2)圆
的方程;(2)圆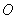 与
与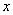 轴相交于
轴相交于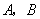 两点,圆内的动点
两点,圆内的动点 使
使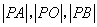 成等比数列,求
成等比数列,求 的取值范围
的取值范围
已知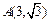 ,O是原点,点P(x, y)的坐标满足
,O是原点,点P(x, y)的坐标满足

(1)求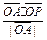 的最大值.;(2)求
的最大值.;(2)求 的取值范围.
的取值范围.