某地需要修建一条大型输油管道通过240公里宽的沙漠地带,该段输油管道两端的输油站已建好,余下工程是在该段两端已建好的输油站之间铺设输油管道和等距离修建增压站(又称泵站).经预算,修建一个增压站的工程费用为400万元,铺设距离为 公里的相邻两增压站之间的输油管道费用为
公里的相邻两增压站之间的输油管道费用为 万元.设余下工程的总费用为
万元.设余下工程的总费用为 万元.
万元.
(1)试将 表示成
表示成 的函数;
的函数;
(2)需要修建多少个增压站才能使 最小,其最小值为多少?
最小,其最小值为多少?
(本小题满分10分)选修4—5:不等式选讲
已知函数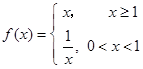 ,
,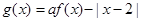 ,
,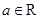 .
.
(Ⅰ)当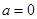 时,若
时,若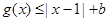 对任意
对任意 恒成立,求实数b的取值范围;
恒成立,求实数b的取值范围;
(Ⅱ)当 时,求函数
时,求函数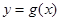 的最小值.
的最小值.
(本小题满分10分)选修4—4:坐标系与参数方程
在极坐标系中曲线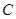 的极坐标方程为
的极坐标方程为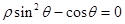 ,点
,点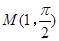 . 以极点O为原点,以极轴为x
. 以极点O为原点,以极轴为x
轴正半轴建立直角坐标系.斜率为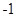 的直线l过点M,且与曲线C交于A,B两点.
的直线l过点M,且与曲线C交于A,B两点.
(Ⅰ)求出曲线C的直角坐标方程和直线l的参数方程;
(Ⅱ)求点M到A,B两点的距离之积.
(本小题满分10分)选修4—1:几何证明选讲
如图,在△ABC中,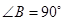 ,以
,以 为直径的⊙O交
为直径的⊙O交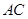 于
于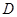 ,过点
,过点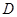 作⊙O的切线交
作⊙O的切线交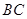 于
于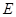 ,
,
交⊙O于点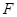 .
.
(Ⅰ)证明: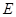 是
是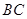 的中点;
的中点;
(Ⅱ)证明: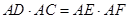 .
.
(本小题满分12分)设函数 .
.
(Ⅰ)讨论函数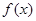 的单调性;
的单调性;
(Ⅱ)如果对所有的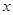 ≥0,都有
≥0,都有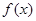 ≤
≤ ,求
,求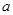 的最小值;
的最小值;
(Ⅲ)已知数列 中,
中, ,且
,且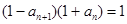 ,若数列
,若数列 的前n项和为
的前n项和为 ,求证:
,求证: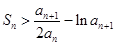 .
.
(本小题满分12分)已知椭圆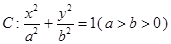 的左、右焦点分别为
的左、右焦点分别为 、
、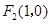 ,过
,过 的直线l与椭圆C相交于A,B两点,且△
的直线l与椭圆C相交于A,B两点,且△ 的周长为
的周长为 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点 作与直线l平行的直线m,且直线m与抛物线
作与直线l平行的直线m,且直线m与抛物线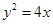 交于P、Q两点,若A、P在x轴
交于P、Q两点,若A、P在x轴
上方,直线PA与直线QB相交于x轴上一点M,求直线l的方程.