如图,已知AB∥CD,∠AEC=90°,那么∠A与∠C的度数和为多少度?为什么?
解:∠A与∠C的度数和为 _________ .
理由:过点E作EF∥AB,
∵EF∥AB,
∴∠A+∠AEF=180°( _________ ).
∵AB∥CD( _________ ),EF∥AB,
∴EF∥CD( _________ )
∴ _________ (两直线平行,同旁内角互补)
∴∠A+∠AEF+∠CEF+∠C= _________ °(等式的性质)
即∠A+∠AEC+∠C= _________ °
∵∠AEC=90°(已知)
∴∠A+∠C= _________ °(等式的性质).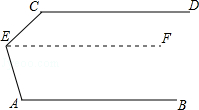
如图:在梯形ABCD中,AD//BC,AD=2,AC=4,BC=6,BD=8,求梯形ABCD的面积。
请在图①的正方形ABCD内,画出使∠APB=90°的一个点P。
请在图②的正方形ABCD内(含边),画出使∠APB=60°的所有的点P。
如图③,现在一块矩形钢板ABCD,AB=4,BC=3,工人师傅想用它裁出两块全等的、面积最大的△APB和△CP
 D钢板,且∠APB=∠CP
D钢板,且∠APB=∠CP D=60°,请你在图③中画出符合要求的点P和P
D=60°,请你在图③中画出符合要求的点P和P

如图1,在平面直角坐标系中,拋物线y=ax2+c与x轴正半轴交于点F(16,0)、与y轴正半轴交于点E(0,16),边长为16的正方形ABCD的顶点D与原点O重合,顶点A与点E重合,顶点C与点F重合;求拋物线的函数表达式
如图2,若正方形ABCD在平面内运动,并且边BC所在的直线始终与x轴垂直,抛物线始终与边AB交于点P且同时与边CD交于点Q(运动时,点P不与A、B两点重合,点Q不与C、D两点重合)。设点A的坐标为(m,n) (m>0)。
j当PO=PF时,分别求出点P和点Q的坐标;
k在j的基础上,当正方形ABCD左右平移时,请直接写出m的取值范围;
l当n=7时,是否存在m的值使点P为AB边中点。若存在,请求出m的值;若不存在,请说明理由。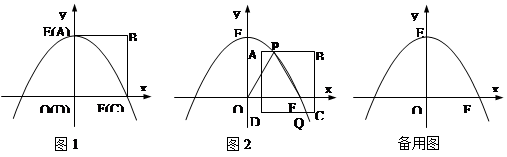
如图1,在△ABC中,点P为BC边中点,直线a绕顶点A旋转,若B、P在直线a的异侧,BM^直线a于点M,CN^直线a于点N,连接PM、PN延长MP交CN于点E(如图2)。j求证:△BPM@△CPE;k求证:PM = PN;
若直线a绕点A旋转到图3的位置时,点B、P在直线a的同侧,其它条件不变。此时PM=PN还成立吗?若成立,请给予证明;若不成立,请说明理由;
若直线a绕点A旋转到与BC边平行的位置时,其它条件不变。请直接判断四边形MBCN的形状及此时PM=PN还成立吗?不必说明理由。
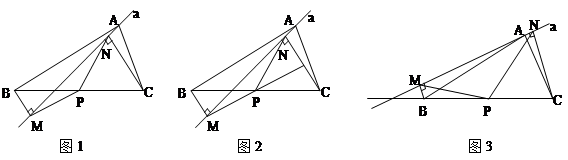
某商人开始时,将进价为每件8元的某种商品按每件10元出售,每天可售出100件.他想采用提高售价的办法来增加利润,经试验,发现这种商品每件每提价l元,每天的销售量就会减少10件.写出售价x(元/件)与每天所得的利润y(元)之间的函数关系式;
每件售价定为多少元,才能使一天的利润最大