如图1,在△ABC中,点P为BC边中点,直线a绕顶点A旋转,若B、P在直线a的异侧,BM^直线a于点M,CN^直线a于点N,连接PM、PN
延长MP交CN于点E(如图2)。j求证:△BPM@△CPE;k求证:PM = PN;
若直线a绕点A旋转到图3的位置时,点B、P在直线a的同侧,其它条件不变。此时PM=PN还成立吗?若成立,请给予证明;若不成立,请说明理由;
若直线a绕点A旋转到与BC边平行的位置时,其它条件不变。请直接判断四边形MBCN的形状及此时PM=PN还成立吗?不必说明理由。
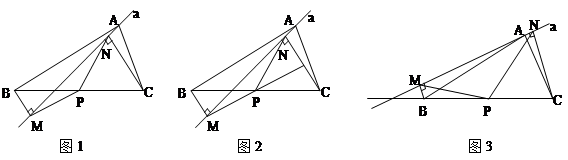
“五一”将至,某商场计划进A、B两种型号的衬衣共80件,商场用于买衬衣的资金不少于4288元,但不超过4300元。两种型号的衬衣进价和售价如下表: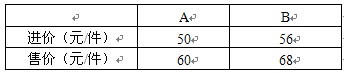
(1)该商场对这种型号的衬衣有哪几种进货方案。
(2)该商场如何获得利润最大。
(3)现据商场测算,每件B型衬衣的售价不会改变,每件A型衬衣的售价将会提高m元(m>0),且所有的衬衣可全部售出,该商场又将如何进货才能满足获得利润最大。(注:利润=售价-成本)
有一客轮往返于重庆和武汉之间,第一次做往返航行时,长江的水流速度为a千米/小时;第二次做往返航行时,正遇上长江发大水,水流速度为b千米/小时(b>a)。已知该船在两次航行中,静水速度都为V千米/小时,问该船两次往返航行所花时间是否相等,若你认为相等,请说明理由;若你认为不相等,请分别表示出两次航行所花的时间,并指出哪次时间更短些?
仔细阅读《战鸽总动员》中的对话,并回答问题。
根据对话内容判断,小B超过最高时速了吗?为什么?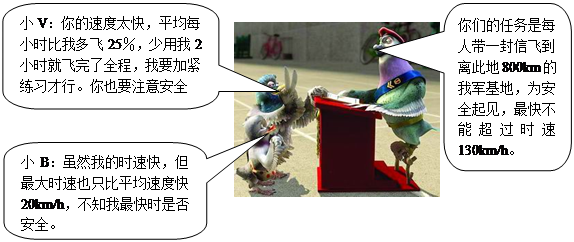
为了测量学校一棵参天古树的高度,我校数学兴趣小组做了如下探索:
实践1:利用一根标竿和一根皮尺设计出如图1的测量方案,把长为2.5米的标竿竖直插入离树(AB)8.7米的点E处,然后沿着直线BE后退到点D,这时眼睛恰好通过标竿顶点F,看到树的顶点A。再用皮尺测得DE=2.7米。观察者目高CD=1.6米。他们利用相似原理求得树高为5.4米。
实践2:提供选用的测量工具有①皮尺一根、②教学用三角板一副、③镜子一面、④测角仪一个。请你设计测量方案,并根据你所设计的测量方案回答下列问题。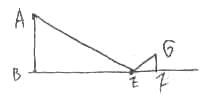
(1)在你设计的方案中,选用的测量工具是(用工具的序号填写)。
(2)在图2中画出你测量方案的示意图。
(3)你需要测得示意图中哪些数据。并分别用a、b、c等表示测得数据。
(4)写出求树高(AB)的等式,AB=。(用a、b、c等字母表示)
先化简,再选择你喜欢的数代入求值