如图,∠1=∠ABC,∠2=∠3,FG⊥AC于F,判断BE与AC有怎样的位置关系,并说明理由。
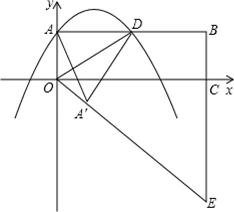
如图,在平面直角坐标系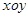 中,矩形
中,矩形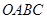 的边
的边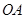 、
、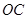 分别在
分别在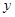 轴和
轴和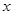 轴的正半轴上,且长分别为
轴的正半轴上,且长分别为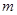 、
、
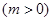 ,
, 为边
为边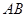 的中点,一抛物线
的中点,一抛物线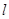 经过点
经过点 、
、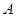 及点
及点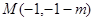 .
.
(1)求抛物线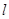 的解析式(用含
的解析式(用含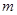 的式子表示);[来#&%^源:@中教网]
的式子表示);[来#&%^源:@中教网]
(2)把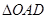 沿直线
沿直线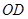 折叠后点
折叠后点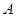 落在点
落在点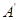 处,连接
处,连接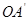 并延长与线段
并延长与线段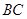 的延长线交于点
的延长线交于点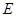 ,若抛物线
,若抛物线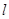 与线段
与线段 相交,求实数
相交,求实数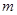 的取值范围;
的取值范围;
(3)在满足(2)的条件下,求出抛物线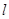 顶点
顶点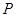 到达最高位置时的坐标.
到达最高位置时的坐标.
如图,在直角坐标系中,点A的坐标为(-2,0),点B的坐标为(1,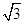 ),已知抛物线y=ax2+bx+c(a≠0)经过三点A、B、O (O为原点).
),已知抛物线y=ax2+bx+c(a≠0)经过三点A、B、O (O为原点).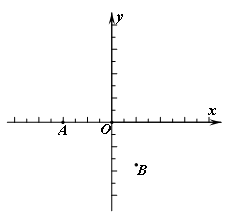
(1)求抛物线的解析式;
(2)在该抛物线的对称轴上,是否存在点C,使△BOC的周长最小.若存在,求出点C的坐标.若不存在,请说明理由;
(3)如果点P是该抛物线上x轴上方的一个动点,那么△PAB是否有最大面积.若有,求出此时P点的坐标及△PAB的最大面积;若没有,请说明理由.(注意:本题中的结果均保留根号).
如图①,已知抛物线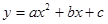 经过点A(0,3),B(3,0),C(4,3).
经过点A(0,3),B(3,0),C(4,3).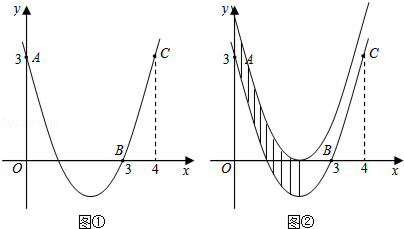
(1)求抛物线的函数表达式;
(2)求抛物线的对称轴和顶点坐标;
(3)把抛物线向上平移,使得顶点落在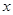 轴上,直接写出两条抛物线、对称轴和
轴上,直接写出两条抛物线、对称轴和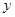 轴围成的图形的面积
轴围成的图形的面积 (图②中阴影部分).
(图②中阴影部分).
某商店购进600个旅游纪念品,进价为每个6元,第一周以每个10元的价格售出200个,第二周若按每个10元的价格销售仍可售出200个,但商店为了适当增加销量,决定降价销售(根据市场调查,单价每降低1元,可多售出50个,但售价不得低于进价),单价降低x元销售一周后,商店对剩余旅游纪念品清仓处理,以每个4元的价格全部售出,如果这批旅游纪念品共获利1250元,问第二周每个旅游纪念品的销售价格为多少元?
用6m长的铝合金型材做一个形状如图所示的矩形窗框,应做成长、宽各为多少时,才能使做成的窗框的透光面积为1.44m2?(设窗框宽为xm)