图1是李晨在一次课外活动中所做的问题研究：他用硬纸片做了两个三角形，分别为△ABC和△DEF，其中∠B=90°，∠A=45°，BC=
，∠F=90°，∠EDF=30°， EF=2．将△DEF的斜边DE与△ABC的斜边AC重合在一起，并将△DEF沿AC方向移动．在移动过程中，D、E两点始终在AC边上(移动开始时点D与点A重合)．
（1）请回答李晨的问题：若CD=10，则AD= ；
（2）如图2，李晨同学连接FC，编制了如下问题，请你回答：
①∠FCD的最大度数为 ；
②当FC∥AB时，AD= ；
③当以线段AD、FC、BC的长度为三边长的三角形是直角三角形，且FC为斜边时，AD= ;
④△FCD的面积s的取值范围是 .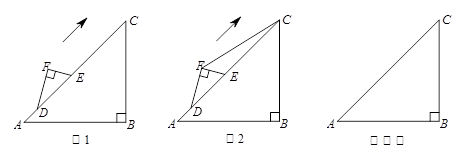
某商场出售一批进价为2元的贺卡，在市场营销中发现此商品的日销售单价x元与日销售量y个之间有如下关系：
| x (元) |
3 |
4 |
5 |
6 |
| y (个) |
20 |
15 |
12 |
10 |
①请你认真分析表中数据，从你所学习过的一次函数、反比例函数和其它函数中确定哪种函数能表示其变化规律，说明确定是这种函数而不是其它函数的理由，并求出它的解析式；
②设经营此贺卡的销售利润为W元，试求出W（元）与x（元）之间的函数关系式. 若物价局规定此贺卡的售价最高不能超过10元/个，请你求出当日销售单价x定为多少元时，才能获得最大日销售利润？
如图，直线AB与双曲线的一个交点为点C，
轴于点D，OD＝2OB＝4OA＝4． 求一次函数和反比例函数的解析式．
已知: 如图, 在□ABCD中, E、F是对角线AC上的两点,且AE = CF.
求证: 四边形BFDE是平行四边形
如图
ABCD中, ∠C=90度，沿着直线BD折叠，使点C落在
处，
交AD于E，
，
，求DE的长．
已知
，求
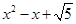的值．