如图1，正方形ABCD与正方形AEFG的边AB、AE（AB＜AE）在一条直线上，正方形AEFG以点A为旋转中心逆时针旋转，设旋转角为
. 在旋转过程中，两个正方形只有点A重合，其它顶点均不重合，连接BE、DG.
（1）当正方形AEFG旋转至如图2所示的位置时，求证：BE=DG；
（2）当点C在直线BE上时，连接FC，直接写出∠FCD 的度数；
（3）如图3，如果=45°，AB =2，AE=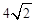
，求点G到BE的距离.
已知A（
，0），直线
与x轴交于点F，与y轴交于点B，直线l∥AB且交y轴于点C，交x轴于点D，点A关于直线l的对称点为A′，连接AA′、A′D．直线l从AB出发，以每秒1个单位的速度沿y轴正方向向上平移，设移动时间为t．
（1）求点A′的坐标（用含t的代数式表示）；
（2）求证：AB＝AF；
（3）过点C作直线AB的垂线交直线于点E，以点C为圆心CE为半径作⊙C，求当t为何值时，⊙C与△AA′D三边所在直线相切？
如图，AB是⊙O的直径，AB＝4，过点B作⊙O的切线，C是切线上一点，且BC＝2，P是线段OA上一动点，连结PC交⊙O于点D，过点P作PC的垂线，交切线BC于点E，交⊙O于点F，连结DF交AB于点G．
（1）当P是OA的中点时，求PE的长；
（2）若∠PDF＝∠E，求△PDF的面积．
把球放在长方体纸盒内，球的一部分露出盒外，如下所示为正视图.已知EF＝CD＝16厘米，求出这个球的半径．
已知
ABCD的两边AB、AD的长是关于x的方程
的两个实数根.
（1）当m为何值时，四边形ABCD是菱形？求出这时菱形的边长；
（2）若AB的边长为2，那么ABCD的周长是多少？
省射击队为从甲、乙两名运动员中选拔一人参加全国比赛，对他们进行了六次测试，测试成绩如下表（单位：环）：
| 第一次 |
第二次 |
第三次 |
第四次 |
第五次 |
第六次 |
|
| 甲 |
10 |
8 |
9 |
8 |
10 |
9 |
| 乙 |
10 |
7 |
10 |
10 |
9 |
8 |
（1）根据表格中的数据，计算出甲的平均成绩是环，乙的平均成绩是环；
（2）分别计算甲、乙六次测试成绩的方差；
（3）根据（1）、（2）计算的结果，你认为推荐谁参加全国比赛更合适，请说明理由．
计算方差的公式：s2＝
[(x1－
)2＋(x2－)2＋＋(xn－)2]