无论k取任何实数,对于直线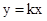 都会经过一个固定的点
都会经过一个固定的点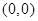 ,我们就称直线
,我们就称直线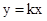 恒过定点
恒过定点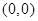 .
.
(1)无论 取任何实数,抛物线
取任何实数,抛物线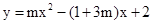 恒过定点
恒过定点 ,直接写出定点A的坐标;
,直接写出定点A的坐标;
(2)已知△ABC的一个顶点是(1)中的定点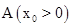 ,且∠B,∠C的角平分线分别是y轴和直线
,且∠B,∠C的角平分线分别是y轴和直线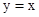 ,求边BC所在直线的表达式;
,求边BC所在直线的表达式;
(3)求△ABC内切圆的半径.
已知:如图,在矩形ABCD中,AF=BE.求证:DE=CF;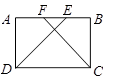
先化简再求值: 其中a=3
其中a=3
计算:
已知:抛物线 与
与 轴交于A(1,0)和B(
轴交于A(1,0)和B( ,0)点,与
,0)点,与 轴交于C点
轴交于C点
(1)求出抛物线的解析式;
(2)设抛物线对称轴与 轴交于M点,在对称轴上是否存在P点,使
轴交于M点,在对称轴上是否存在P点,使 为等腰三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;
为等腰三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;
(3)若点E为第二象限抛物线上一动点,连接BE,CE,求四边形BOCE面积的最大值,并求此时点E 的坐标.
已知:在梯形 中,
中, 点
点 是
是 的中点,
的中点, 是正三角形.动点P、Q分别在线段
是正三角形.动点P、Q分别在线段 和
和 上运动,且∠MPQ=60°保持不变.
上运动,且∠MPQ=60°保持不变.
(1)求证:△BMP∽△CPQ
(2)设PC= ,MQ=
,MQ= 求
求 与
与 的函数关系式;
的函数关系式;
(3)在(2)中,当 取最小值时,判断
取最小值时,判断 的形状,并说明理由.
的形状,并说明理由.