如图,正方形ABCD的边长为6,E是边BC上的一点,△ABE经过旋转后得到△ADF.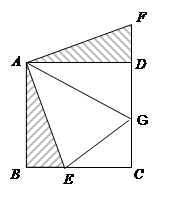
(1)旋转中心是点 ;旋转角最少是 度;
(2)求四边形AECF的面积;
(3)如果点G在边CD上,且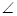 GAE=450,
GAE=450,
①试判断GE、BE、DG之间有什么样的数量关系?并说明理由。
②若BE=2,求DG的长。
如图,在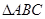 中,AB=AC,以AB为直径的
中,AB=AC,以AB为直径的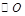 交BC于点M,
交BC于点M,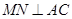 于点N.
于点N.
(1)求证:MN是⊙O的切线;
(2)若 ,AB=2,求图中阴影部分的面积.
,AB=2,求图中阴影部分的面积.
A、B两地间的距离为15千米,甲从A地出发步行前往B地,20分钟后,乙从 B地出发骑车前往A地,且乙骑车比甲步行每小时多走10千米.乙到达A地后停留40分钟,然后骑车按原路原速返回,结果甲、乙两人同时到达B地.求甲从A地到B地步行所用的时间.
如图,△ABC中,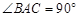 ,延长BA至D,使
,延长BA至D,使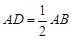 ,点E、F分别是边BC、AC的中点.
,点E、F分别是边BC、AC的中点.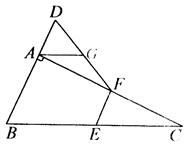
(1)判断四边形DBEF的形状并证明;
(2)过点A作AG⊥BC交DF于G,求证:AG=DG.
已知甲同学手中藏有三张分别标有数字 ,
,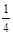 ,1的卡片,乙同学手中藏有三张分别标有数字1,3,2的卡片,卡片外形相同.现从甲乙两人手中各任取一张卡片.
,1的卡片,乙同学手中藏有三张分别标有数字1,3,2的卡片,卡片外形相同.现从甲乙两人手中各任取一张卡片.
(1)请你用树形图或列表法列出所有可能的结果;
(2)求抽出的两张卡片数字积恰好为1的概率.
在射击竞赛的选拔赛中,运动员甲10次射击成绩的统计表和扇形统计图如下:
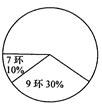
(1)根据统计表(图)中提供的信息,补全统计表及扇形统计图;
(2)已知乙运动员10次射击的平均成绩为9环,方差为1.2,如果只能选一人参加比赛,你认为应该派谁去?并说明理由.