如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y= x2+bx+c经过点B,且顶点在直线x=
x2+bx+c经过点B,且顶点在直线x= 上.
上.
(1)求抛物线对应的函数关系式;
(2)若把△ABO沿x轴向右平移得到△DCE,点A、B、O的对应点分别是D、C、E,当四边形ABCD是菱形时,试判断点C和点D是否在该抛物线上,并说明理由;
(3)在(2)的条件下,连接BD,已知对称轴上存在一点P使得△PBD的周长最小,求出P点的坐标;
(4)在(2)、(3)的条件下,若点M是线段OB上的一个动点(点M与点O、B不重合),过点M作MN∥BD交x轴于点N,连接PM、PN,设OM的长为t,△PMN的面积为S,求S和t的函数关系式,并写出自变量t的取值范围,S是否存在最大值?若存在,求出最大值和此时M点的坐标;若不存在,说明理由.
某西瓜经营户以2元/千克的价格购进一批小型西瓜,以3元/千克的价格出售,每天可售出200千克。为了促销,该经营户决定降价销售。经调查发现,这种小型西瓜每降价0.1元/千克,每天可多售出40千克。另外每天的房租等固定成本共24元。该经营户要想每天盈利200元,应将每千克小型西瓜的售价降低多少元?
如图,在4×3的网格上,由个数相同的白色方块与黑色方块组成一幅图案,请仿照此图案,在下列网格中分别设计出符合要求的图案(注:①不得与原图案相同;②黑、白方块的个数要相同).
某市对电话费作了调整,原市话费为:每3分钟0.2元(不足3分钟按3分钟计算);现调整为:前3分钟为0.2元,以后每分钟加收0.1(不足1分钟按1分钟计算).设通话时间x分钟时,调整前话费为a元,调整后话费为b元.
⑴ 填写下表
| x |
4 |
4.2 |
5.8 |
6.3 |
7.1 |
11 |
| a |
||||||
| b |
⑵ 指出 取何值时,
取何值时,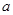 不超过
不超过 ;(直接写出答案,不需要解答过程)
;(直接写出答案,不需要解答过程)
⑶ 当 时,请你按调整后的收费方法设计两种通话方案(可以分几次拨打),使所需话费
时,请你按调整后的收费方法设计两种通话方案(可以分几次拨打),使所需话费 满足关系式:
满足关系式: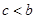 .
.
2010年4月14日7时49分在我国青海省玉树发生里氏7.1级的强烈地震,灾情牵动全国人民的心,“大爱无疆,心系玉树”。某地区计划为灾人民区搭建A、B两种型号的帐篷300顶,其中A型帐篷可供3人居住;B型帐篷可供10人居住,正好可供2300人临时居住。
(1)求该地区搭建A型、B型帐篷各多少间?
(2)该地区计划租用甲乙两种型号的卡车共20辆将这批帐篷紧急送往灾区,已知甲型卡车每辆可同时装运4顶A帐篷和11顶B帐篷;乙型卡车每辆可同时装运12顶A帐篷和7顶B帐篷。能否安排甲乙两种卡车恰好一次性将这批帐篷送往灾区?如果不能,请你说出一种方案把这批帐篷一次性运往灾区(只要写出一种即可)?
如图,在△ABC中,AD⊥BC,AD=BD,DE=DC,延长BE交AC于F,
(1)试说明△BDE≌△ADC的理由;
(2)你能说出BE与AC的数量和位置关系吗?并说明理由.
(3)△BDE通过怎样的图形变换变到△ADC的位置的.试用语言描述.