已知：直线yx1经过点B（2，n），且与x轴交于点A.(1)-优题课

游客

题文

已知：直线y=x+1经过点B（2，n），且与x轴交于点A.
(1)求n及点A坐标.
(2) 若点P是x轴上一点,且△APB的面积为6,求点P的坐标.

科目数学题型解答题难度较易

知识点：一次函数的最值

登录免费查看答案和解析

相关试题

如图，▱ABCD中，点E，F在对角线BD上，且BE=DF，求证：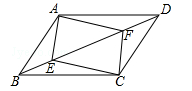

（1）AE=CF；
（2）四边形AECF是平行四边形．

如图，抛物线与x轴交于点 $A （ - \frac{1}{3} ， 0 ）$ 、点 $B （ 2 ， 0 ）$ ，与 $y$ 轴交于点 $C （ 0 ， 1 ）$ ，连接BC．

（1）求抛物线的函数关系式；
（2）点 $N$ 为抛物线上的一个动点，过点 $N$ 作 $N P ⊥ x$ 轴于点 $P$ ，设点N的横坐标为 $t (- \frac{1}{3} < t < 2)$ ，求 $△ A B N$ 的面积S与t的函数关系式；
（3）若 $- \frac{1}{3} < t < 2$ 且 $t \neq 0$ 时 $△ O P N ~ △ C O B$ ，求点 $N$ 的坐标．

如图，在△ACE中，CA=CE，∠CAE=30°，⊙O经过点C，且圆的直径AB在线段AE上．

（1）试说明CE是⊙O的切线；
（2）若△ACE中AE边上的高为h，试用含h的代数式表示⊙O的直径AB；
（3）设点D是线段AC上任意一点（不含端点），连接OD，当CD+OD的最小值为6时，求⊙O的直径AB的长．

（1）填空：=；
=；
=．
（2）猜想：=（其中n为正整数，且）．
（3）利用（2）猜想的结论计算：．

（本小题满分9分）我市准备在相距2千米的M，N两工厂间修一条笔直的公路，但在M地北偏东45°方向、N地北偏西60°方向的P处，有一个半径为0.6千米的住宅小区（如图），问修筑公路时，这个小区是否有居民需要搬迁？（参考数据：≈1.41，≈1.73）

试卷网试题网古诗词网作文网范文网