如图,在平面直角坐标系中,点O坐标原点,直线l分别交x轴、y轴于A,B两点,OA<OB,且OA、OB的长分别是一元二次方程 的两根.
的两根.
(1)求直线AB的函数表达式;
(2)点P是y轴上的点,点Q第一象限内的点.若以A、B、P、Q为顶点的四边形是菱形,请直接写出Q的坐标.
如图,AB•AC=AD•AE,且∠1=∠2,求证:△ABC∽△AED.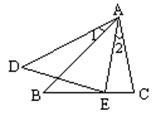
(1)计算:
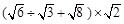 .
. (2)解方程:
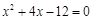
(14分)已知抛物线y=ax2+bx+c(a≠0)经过A(-2,0)、B(0,1)两点,且对称轴是y轴.经过点C(0,2)的直线l与x轴平行,O为坐标原点,P、Q为抛物线y=ax2+bx+c(a≠0)上的两动点.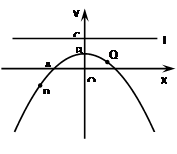
(1) 求抛物线的解析式;
(2) 以点P为圆心,PO为半径的圆记为⊙P,判断直线l与⊙P的位置关系,并证明你的结论;
(3) 设线段PQ=9,G是PQ的中点,求点G到直线l距离的最小值.
(13分)如图,在△ABC中,AB=AC=5,BC=6,点D为AB边上的一动点(D不与A、B重合),过D作DE∥BC,交AC于点E.把△ADE沿直线DE折叠,点A落在点A'处.连结BA',设AD=x,△ADE的边DE上的高为y.(1) 求出y与x的函数关系式;
(2) 若以点A'、B、D为顶点的三角形与△ABC 相似,求x的值;
(3) 当x取何值时,△A' DB是直角三角形.

(12分)某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于50%,经试销发现,销售量y(件)与销售单价x(元)的关系符合一次函数y=-x+140.(1) 直接写出销售单价x的取值范围.
(2) 若销售该服装获得利润为W元,试写出利润W与销售单价x之间的关系式;销售单价为多少元时,可获得最大利润,最大利润是多少元?
(3) 若获得利润不低于1200元,试确定销售单价x的范围.